ฮฮตฮฌฯฮตฮนฯ: 6.075
ฮคฮฟฯ
ฮฮฏฮบฮฟฯ
ฮฮฑฯฯฮฝฯฮต
ยซฮ ฯฮนฮฝ ฮฑฯโ ฯฮปฮฑ ฯฯฮญฯฮตฮน ฮฝฮฑ ฮดฮนฮฑฯฯ
ฯฯฮฝฮฟฯ
ฮผฮต ฯฮฑ ฯฯฮฟฮฒฮปฮฎฮผฮฑฯฮฑ.ย ฮฮฑฮน ฯฮฑฯฮฌ ฯฮฑ ฮปฮตฮณฯฮผฮตฮฝฮฑ, ฯฯฮทฮฝ ฮตฯฮนฯฯฮทฮผฮฟฮฝฮนฮบฮฎ ฮถฯฮฎ ฯฮฑ ฯฯฮฟฮฒฮปฮฎฮผฮฑฯฮฑ ฮดฮตฮฝ ฯฮฏฮธฮตฯฮฑฮน ฮฑฯฯ ฮผฯฮฝฮฑ ฯฮฟฯ
ฯ. ฮฮนฮฑ ฯฮฟ ฮตฯฮนฯฯฮทฮผฮฟฮฝฮนฮบฯ ฯฮฝฮตฯฮผฮฑ ฮบฮฌฮธฮต ฮณฮฝฯฯฮท ฮตฮฏฮฝฮฑฮน ฮฑฯฮฌฮฝฯฮทฯฮท ฯฮต ฮผฮนฮฑ ฮตฯฯฯฮทฯฮท. ฮฮฝ ฮดฮตฮฝ ฯ
ฯฮฎฯฮพฮต ฮตฯฯฯฮทฮผฮฑ ฮดฮตฮฝ ฯ
ฯฮฌฯฯฮตฮน ฮตฯฮนฯฯฮทฮผฮฟฮฝฮนฮบฮฎ ฮณฮฝฯฯฮท.ย
ย ย ย ย ย ย ย ย ย ฮคฮฏฯฮฟฯฮฑ ฮดฮตฮฝ ฮตฮฏฮฝฮฑฮน ฮฑฯ
ฯฮฟฮฝฯฮทฯฮฟ. ฮคฮฑ ฯฮฌฮฝฯฮฑ ฮฟฮนฮบฮฟฮดฮฟฮผฮฟฯฮฝฯฮฑฮนยป
ฮฯฯฯฯฮฑฯฮผฮฑ ฮฑฯฯ ฯฮฟ ฮฒฮนฮฒฮปฮฏฮฟย ยซฮ ฮดฮนฮฑฮผฯฯฯฯฯฮท ฯฮฟฯ
ฮตฯฮนฯฯฮทฮผฮฟฮฝฮนฮบฮฟฯ ฯฮฝฮตฯฮผฮฑฯฮฟฯยปย ฯฮฟฯ
ฮฮฌฮปฮปฮฟฯ
ฮตฯฮนฯฯฮฎฮผฮฟฮฝฮฑ ฮบฮฑฮน ฯฮนฮปฮฟฯฯฯฮฟฯ
Gaston Bachelard
ฮฮนฯฮฑฮณฯฮณฮฎ
ฮฮน ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮฟฯ
ฮดฮฏฮฝฮฟฮฝฯฮฑฮน ฯฯฮฟฯ
ฯ ฮผฮฑฮธฮทฯฮญฯ ฮฮฮฯ
ฮบฮตฮฏฮฟฯ
ฮผฮต ฮธฮญฮผฮฑ ฯฮนฯ ฮณฯฮฑฯฮนฮบฮญฯ ฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯ ฯฯฮฟฮฝ ฯฮฟฮผฮญฮฑ ฯฮทฯ ฮฮนฮฝฮทฮผฮฑฯฮนฮบฮฎฯ, ฯฮฑฯฮฑฮผฮญฮฝฮฟฯ
ฮฝ ฯฯฮตฮดฯฮฝ ฮฑฮฝฮฑฮปฮปฮฟฮฏฯฯฮตฯ ฮตฮดฯ ฮบฮฑฮน ฯฮฟฮปฮปฮฌ ฯฯฯฮฝฮนฮฑ. ฮคฮฟ ฮฏฮดฮนฮฟ ฮฑฮบฯฮนฮฒฯฯ ฯฯ
ฮผฮฒฮฑฮฏฮฝฮตฮน ฮบฮฑฮน ฮผฮต ฯฮนฯ ฮตฯฮนฮดฮนฯฮบฯฮผฮตฮฝฮตฯ ฮนฮบฮฑฮฝฯฯฮทฯฮตฯ ฯฮฟฯ
ฯฯฮฟฯฮดฮฟฮบฮฟฯฮผฮต ฮฝฮฑ ฮฑฯฮฟฮบฯฮฎฯฮฟฯ
ฮฝ ฮฟฮน ฮผฮฑฮธฮทฯฮญฯ.
ฮฮฑฯฮฌ ฯฮท ฮณฮฝฯฮผฮท ฮผฮฟฯ
, ฮฑฯ
ฯฯ ฮฟฯฮตฮฏฮปฮตฯฮฑฮน ฯฮต ฮผฮตฮณฮฌฮปฮฟ ฮฒฮฑฮธฮผฯ ฮบฮฑฮน ฯฯฮฟ ฮณฮตฮณฮฟฮฝฯฯ ฯฯฮน ฯฯฮท ฮดฮนฮดฮฑฯฮบฮฑฮปฮฏฮฑ ฮผฮฑฯ, ฯฯฯฯ ฮบฮฑฮน ฯฯฮนฯ ฮตฮพฮตฯฮฌฯฮตฮนฯ, ฮฟฮน ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮฒฮฑฯฮฏฮถฮฟฮฝฯฮฑฮน ฯฯฮฑ ฮผฮญฯฮฑ ฯฮฟฯ
ฮบฯ
ฯฮฏฯฯ ฯฯฮทฯฮนฮผฮฟฯฮฟฮนฮฟฯฮผฮต: ฯฮฟฮฝ ฮบฮนฮผฯฮปฮนฮฟฯฮฏฮฝฮฑฮบฮฑ, ฯฮฟ ฯฯฮฟฮปฮนฮบฯ ฮตฮณฯฮตฮนฯฮฏฮดฮนฮฟ ฮบฮฑฮน ฯฮฟ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ ยซฯฮฑฯฯฮฏ-ฮผฮฟฮปฯฮฒฮนยป.
ฮฮฝ ฮตฯฮนฮธฯ
ฮผฮฟฯฮผฮต ฯฮทฮฝ ฮฑฮฝฮฑฮฝฮญฯฯฮท ฯฮฟฯ
ฯฮตฯฮตฯฯฮฟฯฮฏฮฟฯ
ฯฯฮฝ ฮดฯฮฑฯฯฮทฯฮนฮฟฯฮฎฯฯฮฝ ฮบฮฑฮน ฯฯฮฝ ฯฯฯฯฯฮฝ ฮดฮนฮดฮฑฯฮบฮฑฮปฮฏฮฑฯ ฮผฮฑฯ ฮดฮตฮฝ ฮญฯฮฟฯ
ฮผฮต ฯฮฑฯฮฌ ฮฝฮฑ ฯฯฯฮญฯฮฟฯ
ฮผฮต ฯฮฟ ฮตฮฝฮดฮนฮฑฯฮญฯฮฟฮฝ ฮผฮฑฯ ฯฮต ยซฮผฮนฮบฯฮฌ ฮตฮพฮตฮนฮดฮนฮบฮตฯ
ฮผฮญฮฝฮฑ ฮผฮนฮบฯฮฌ ฯฯฮฟฮณฯฮฌฮผฮผฮฑฯฮฑยป (applets Scratch) ฯฮฟฯ
ฯฯฮญฯฮฟฯ
ฮฝ ฮฑฯฮตฯ
ฮธฮตฮฏฮฑฯ ฯฯฮฟ ฮดฮนฮฑฮดฮฏฮบฯฯ
ฮฟ ฮบฮฑฮน ฮฒฮญฮฒฮฑฮนฮฑ ฮผฯฮฟฯฮฟฯฮฝ ฮฝฮฑ ฯฯฮญฮพฮฟฯ
ฮฝ “ฮฑฯ
ฯฯฮฝฮฟฮผฮฑ” ฯฯฮฟฮฝ ฯ
ฯฮฟฮปฮฟฮณฮนฯฯฮฎ ฮผฮฑฯ. ฮฯฯฮน, ฮตฯฮนฯฯ
ฮณฯฮฌฮฝฮตฯฮฑฮน ฯฮฟ ฮผฮตฮณฮฑฮปฯฯฮตฯฮฟ ฮตฯฯฮฟฯ ฯฯฮฝ ฯฯฮฟฯฯฮตฯฮฟฮผฮญฮฝฯฮฝ ฮดฯ
ฮฝฮฑฯฮฟฯฮฎฯฯฮฝ: ฮดฮนฮฑฮดฮฏฮบฯฯ
ฮฟ, ฮฒฮนฮฝฯฮตฮฟฯฯฮฟฮฒฮฟฮปฮญฮฑฯ ฮบฮฑฮน ฮดฮนฮฑฮดฯฮฑฯฯฮนฮบฯฯ ฯฮฏฮฝฮฑฮบฮฑฯ ฯฯฮท ฯฯฮฟฮปฮนฮบฮฎ ฯฮฌฮพฮท ฮฎ ฯฯฮฟ ฮตฯฮณฮฑฯฯฮฎฯฮนฮฟ ฯ
ฯฮฟฮปฮฟฮณฮนฯฯฯฮฝ.
ฮฮผฯฯ, ฮท ฮตฯฮนฮฝฯฮทฯฮท ฮฝฮญฯฮฝ ฮดฯฮฑฯฯฮทฯฮนฮฟฯฮฎฯฯฮฝ ฯฮฟฯ
ฮฝฮฑ ฮฒฮฑฯฮฏฮถฮฟฮฝฯฮฑฮน ฯโ ฮฑฯ
ฯฮฌ ฯฮฑ applets ฮดฮตฮฝ ฮตฮฏฮฝฮฑฮน ฮตฯฮบฮฟฮปฮท ฯ
ฯฯฮธฮตฯฮท. ฮฮนฮฑ ฯฮทฮฝ ฮตฯฮนฮฝฯฮทฯฮฎ ฯฮฟฯ
ฯ ฮฑฯฮฑฮนฯฮตฮฏฯฮฑฮน ฯฯฯฮฟ ฮท ฯฯ
ฮฝฮตฯฮณฮฑฯฮฏฮฑ ฯฯฮฝ ฮตฮบฯฮฑฮนฮดฮตฯ
ฯฮนฮบฯฮฝ ฯฮทฯ ฯฯฮฌฮพฮทฯ ฯฯฮฟ ฮบฮฑฮน ฮท ฮดฮฟฮบฮนฮผฮฑฯฮฏฮฑ ฯฮฟฯ
ฯ ฯฯฮทฮฝ ฯฯฮฑฮณฮผฮฑฯฮนฮบฮฎ ฯฯฮฟฮปฮนฮบฮฎ ฯฮฌฮพฮท. ฮฮฑฮถฮฏ ฮผฮต ฮฑฯ
ฯฮฌ, ฯฮทฮผฮฑฮฝฯฮนฮบฯ ฮตฮฏฮฝฮฑฮน ฮบฮฑฮน ฯฮฟ ฮฝฮฑ ยซฮผฮฟฮนฯฮฑฮถฯฮผฮฑฯฯฮตยป ฯฮนฯ ฮนฮดฮญฮตฯ ฮบฮฑฮน ฯฮนฯ ฯฯฮฟฯฮฌฯฮตฮนฯ ฮผฮฑฯ ฮผฮฑฮถฮฏ ฮผฮต ฮฌฮปฮปฮฟฯ
ฯ ฮตฮบฯฮฑฮนฮดฮตฯ
ฯฮนฮบฮฟฯฯ ฯฯ
ฮผฮผฮตฯฮญฯฮฟฮฝฯฮฑฯ ฯฯฮนฯ ฮผฮนฮบฯฮญฯ ฮฎ ฮผฮตฮณฮฌฮปฮตฯ ยซฮฮฟฮนฮฝฯฯฮทฯฮตฯยป ฯฮฟฯ
ฮตฮผฯฮฑฮฝฮฏฮถฮฟฮฝฯฮฑฮน ฯฯฮฟฮฝ ฮบฯ
ฮฒฮตฯฮฝฮฟฯฯฯฮฟ.
ฮ ฮฒฮฑฯฮนฮบฮฎ ฯ
ฯฯฮธฮตฯฮท ฯฮฟฯ
ฯ
ฯฮฟฯฯฮทฯฮฏฮถฯ ฮดฮตฮฝ ฮตฮฏฮฝฮฑฮน ฮฌฮปฮปฮท ฮฑฯฯ ฮผฮตฯฮนฮบฮญฯ ฮนฮดฮญฮตฯ ฯฮฟฯ
ฮญฯฮฟฯ
ฮฝ ฮดฮนฮฑฯฯ
ฯฯฮธฮตฮฏ ฮฑฮฝฮฑฯฮฟฯฮนฮบฮฌ ฮผฮต ฯฮนฯ ยซฮ ฮฟฮปฮปฮฑฯฮปฮญฯ ฮฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯยป. ฮฯ
ฯฮฏฮฑฯฯฮท ฮธฮตฯฯฯ ฯฮทฮฝ ฮนฮดฮญฮฑ ฯฯฮน ฮท ฮผฮฌฮธฮทฯฮท ฮดฮนฮตฯ
ฮบฮฟฮปฯฮฝฮตฯฮฑฮน ฮฑฮฝ ฮฟฮน ฮผฮฑฮธฮทฯฮญฯ ฮฑฯฮบฮฟฯฮฝฯฮฑฮน ฮผฮต ฮผฮตฯฮฑฮฒฮฌฯฮตฮนฯ ฮฑฯฯ ฯฮท ฮผฮนฮฑ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท ฯฯฮทฮฝ ฮฌฮปฮปฮท ฮฟฯฯฯฮต ฮญฯฯฮน ฮตฮฝฮนฯฯฯฮตฯฮฑฮน ฮบฮฑฮน ฮท ฮฟฮนฮบฮฟฮดฯฮผฮทฯฮท ฯฯฮฝ ฮตฮฝฮฝฮฟฮนฯฮฝ ฮบฮฑฮน ฯฯฮฝ ฮฝฯฮผฯฮฝ ฯฮฟฯ
ฯฮฟฮผฮญฮฑ ยซฮฮนฮฝฮทฮผฮฑฯฮนฮบฮฎยป
(ฮฮปฮญฯฮต ฯฮทฮฝ ฮฑฮฝฮฌฯฯฮทฯฮท ฯฯฮฟ blog ฮผฮฟฯ
ยซฮฮน ฮณฯฮฑฯฮนฮบฮญฯ ฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯ, ฮฟฮน ฮดฯ
ฯฮบฮฟฮปฮฏฮตฯ ฯฯฮฝ ฮผฮฑฮธฮทฯฯฮฝ ฮบฮฑฮน ฮท ฯฮฑฮนฮดฮฑฮณฯฮณฮนฮบฮฎ ฮนฮดฮญฮฑ ฯฯฮฝ ฮผฮตฯฮฑฮฒฮฌฯฮตฯฮฝ ฮฑฯฯ ฮผฮนฮฑ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท ฯฮต ฮฌฮปฮปฮตฯยป (http://makolas.blogspot.com/2011/10/blog-post_15.htmlย ).
ฮฯฮนฯฮปฮญฮฟฮฝ, ฯฯฮนฯ ฯฯฮฟฯฮฌฯฮตฮนฯ ฮผฮฟฯ
ฯ
ฯฮฟฯฯฮทฯฮฏฮถฯ ฯฯฮน ฮธฮฑ ฯฯฮญฯฮตฮน ฮฝฮฑ ฮดฮนฮฑฮผฮฟฯฯฯฯฮฟฯ
ฮผฮต ฯฮฟฯ
ฯ ฮตฮนฮดฮนฮบฮฟฯฯ ฯฯฯฯฮฟฯ
ฯ ฮดฮนฮดฮฑฯฮบฮฑฮปฮฏฮฑฯ ฮบฮฑฮน ฮผฮฌฮธฮทฯฮทฯ ฮญฯฯฮน ฯฯฯฮต ฮฝฮฑ ฮปฮฑฮผฮฒฮฌฮฝฮฟฮฝฯฮฑฮน ฯฮทฯฮฌ ฯ
ฯฯฯฮท ฯฮฑ ฮผฮญฯฮฑ (ฮฎ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝฯฮฑ) ฮตฮฝฮฑฯฯฯฮปฮทฯฮทฯ ฯฯฮฝ ฮผฮฑฮธฮทฯฯฮฝ ฮบฮฑฮธฯฯ ฮบฮฑฮน ฮฟฮน ฮตฮผฯฮปฮตฮบฯฮผฮตฮฝฮตฯ ฮบฮฌฮธฮต ฯฮฟฯฮฌ ฮฑฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯ. ฮฮต ฮฌฮปฮปฮฑ ฮปฯฮณฮนฮฑ ฮฟฮน ฯฯฮฟฯฮตฮนฮฝฯฮผฮตฮฝฮตฯ ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฯฮตฯฮนฮปฮฑฮผฮฒฮฌฮฝฮฟฯ
ฮฝ ฯฯ
ฮฝฮดฯ
ฮฑฯฯฮนฮบฮฌ ฯฯฯฮฟ ฯฮฑ applets ฯฯฮฟ ฮบฮฑฮน ฯฮฑ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝฯฮฑ {ยซฯฮฑฯฯฮฏ โ ฮผฮฟฮปฯฮฒฮนยป ฮบฮฑฮน ยซฮดฮนฮฑฮดฯฮฑฯฯฮนฮบฯฯ ฯฮฏฮฝฮฑฮบฮฑฯยป} ฮผฮต ฯฯ
ฮณฮบฮตฮบฯฮนฮผฮญฮฝฮฟฯ
ฯ ฯฯฯฯฮฟฯ
ฯ ฯฮฟฯ
ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฮดฮนฮฑฯฯ
ฯฯฮฝฮฟฮฝฯฮฑฮน, ฮณฮนฮฑ ฯฮฑฯฮฌฮดฮตฮนฮณฮผฮฑ, ฯฯ ฮตฮพฮฎฯ:

ฮฮฟฮฝฯฮฟฮปฮฟฮณฮฏฯ ฮดฮฏฮฝฮตฯฮฑฮน ฮท ฮตฯ
ฮบฮฑฮนฯฮฏฮฑ ฯฯฮฟฯ
ฯ ฮผฮฑฮธฮทฯฮญฯ ฮฝฮฑ ฮตฮฏฮฝฮฑฮน ฮตฮฝฮตฯฮณฮฟฮฏ ฮบฮฌฮฝฮฟฮฝฯฮฑฯ ฯฯฮฌฮณฮผฮฑฯฮฑ ฮบฮฑฮน ฮฝฮฑ ฯฯ
ฮปฮปฮฟฮณฮฏฮถฮฟฮฝฯฮฑฮน ฯฮตฮนฯฮฑฮผฮฑฯฮนฮถฯฮผฮตฮฝฮฟฮน ฯฮต ฯฯ
ฮณฮบฮตฮบฯฮนฮผฮญฮฝฮฟ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ. ฮฮน ฯฯฮฟฯฮตฮนฮฝฯฮผฮตฮฝฮตฯ ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮดฮฏฮฝฮฟฯ
ฮฝ ฮญฮผฯฮฑฯฮท ฯฯฮฑ ฯฮฟฮนฮฟฯฮนฮบฮฌ ฯฮฑฯฮฑฮบฯฮทฯฮนฯฯฮนฮบฮฌ ฯฮตฯฮนฯฯฯฯฮตฯฮฟ ฮฑฯฯ ฯฯฮน ฯฯฮฑ ฯฮฟฯฮฟฯฮนฮบฮฌ-ฯ
ฯฮฟฮปฮฟฮณฮนฯฯฮนฮบฮฌ. ฮฮนฮฑ ฯฮฑฯฮฌฮดฮตฮนฮณฮผฮฑ, ฮฟฮน ฮผฮฑฮธฮทฯฮญฯ ฮฑฮฝฮฑฯฯฯฮนฮฟฯฮฝฯฮฑฮน ฯฯฮน ฮผฯฮฝฮฟ ฮณฮนฮฑ ฯฮฟ ยซฯฮน ฮตฮฏฮฝฮฑฮนยป ฮตฯ
ฮธฯฮณฯฮฑฮผฮผฮท ฮฟฮผฮฑฮปฮฌ ฮตฯฮนฯฮฑฯฯ
ฮฝฯฮผฮตฮฝฮท ฮบฮฏฮฝฮทฯฮท ฮฑฮปฮปฮฌ ฮบฮฑฮน ฮณฮนฮฑ ฯฮฟ ยซฯฮน ฮดฮตฮฝ ฮตฮฏฮฝฮฑฮนยป ฯฯฯฯ ฯฯฮฝฮนฮถฮต ฮผฮต ฮญฮผฯฮฑฯฮท ฮฟ ฮฮฝฯฯฮญฮฑฯ ฮ. ฮฮฑฯฯฮญฯฮฑฯ.
ฮฃฯฮผฯฯฮฝฮฑ ฮผฮต ฯฮฑ ฯฮฑฯฮฑฯฮฌฮฝฯ ฮฟฮน ฮผฮฑฮธฮทฯฮญฯ ฯฮฌฮฝฯฮฑ ฮญฯฮฟฯ
ฮฝ ฯฯฮท ฮดฮนฮฌฮธฮตฯฮฎ ฯฮฟฯ
ฯ ฮผฮนฮฑ ยซฯฯฮฟฮฒฮปฮทฮผฮฑฯฮนฮบฮฎ ฮบฮฑฯฮฌฯฯฮฑฯฮทยป (ฮญฮฝฮฑ ฯฯฮฝฮฟฮปฮฟ ฯฮปฮทฯฮฟฯฮฟฯฮนฯฮฝ ฮบฮฑฮน ฮบฮฑฮธฮทฮบฯฮฝฯฯฮฝ ฮผฮต ฮผฮฟฯฯฮฎ ฯฮฟฮนฮบฮนฮปฯฮฝ ฮฑฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฯฮฝ ฯฯฯฯ ฮฮตฮบฯฮนฮบฮฎ, ฮฮปฮณฮตฮฒฯฮนฮบฮฎ, ฮ ฮฏฮฝฮฑฮบฮฑฯ ฯฮนฮผฯฮฝ, ฮฯฮฌฯฮทฮผฮฑ ) ฮบฮฑฮน ฯฯฮท ฯฯ
ฮฝฮญฯฮตฮนฮฑ ฯฯฮฟฯฯฯฮฟฯฮฝ ฯฯฮนฯ ฮฑฯฮฑฮฝฯฮฎฯฮตฮนฯ ฯฮฟฯ
ฯ ฮฑฮบฮฟฮปฮฟฯ
ฮธฯฮฝฯฮฑฯ grosso modo ฯฮทฮฝ ฯฮฑฯฮฑฮดฮฟฯฮนฮฑฮบฮฎ ยซฯฮตฮนฯฮฑฮผฮฑฯฮนฮบฮฎ ฮผฮญฮธฮฟฮดฮฟ ฮญฯฮตฯ
ฮฝฮฑฯยป
(ฮฒฮปฮญฯฮต ฮญฮฝฮฑ ฯฮฑฮปฮนฯ ฮฌฯฮธฯฮฟ ฮผฮฟฯ
ยซH ฮญฮฝฯฮฑฮพฮท ฯฮทฯ ยซฮ ฮตฮนฯฮฑฮผฮฑฯฮนฮบฮฎฯ ฮฮตฮธฯฮดฮฟฯ
ฮฯฮตฯ
ฮฝฮฑฯยป ฯฯฮฟ ฮฃฯฮฟฮปฮตฮฏฮฟยปย http://makolas.blogspot.gr/2013/07/h.html ) ฯฯฯฯ ฮญฯฮตฮน ฮบฮฑฮธฮนฮตฯฯฮธฮตฮฏ ฮณฮนฮฑ ฯฮนฯ ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮผฮต ฯฮตฮนฯฮฌฮผฮฑฯฮฑ ฯฯฮฟ ฯฯฮฟฮปฮนฮบฯ ฮตฯฮณฮฑฯฯฮฎฯฮนฮฟ.
ฮคฮตฮปฮนฮบฮฌ, ฮญฯฯฮนฮฑฮพฮฑย ฮญฮฝฮฑ ฮผฮนฮบฯฯ appletย ฯฯฮฟ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ ฯฮฟฯ
Scratch ฮบฮฑฮน ฯฮฑ ฮฑฮฝฮฌฯฯฮทฯฮฑ ฯฯฮฟ Scratch Website: ฮฮพฮนฮฟฯฮฟฮนฮตฮฏ ฯฮฟ project ฯฮฟฯ
ฯฮตฯฮนฮปฮฑฮผฮฒฮฌฮฝฮตฮน ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t), ฯฮฟฮฝ ฯฮฏฮฝฮฑฮบฮฑ ฯฮฑฯฯ
ฯฮฎฯฯฮฝ ฮบฮฑฮน ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฮตฮฝฯฯ ฯฮฑฮนฮดฮนฮฟฯ.
ฮ. ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮผฮต ฯฮฟ applet Scratch ยซฮฯฯ ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t) ฯฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฮบฮฏฮฝฮทฯฮทฯยป (http://scratch.mit.edu/projects/dapontesgr/2202942 )
ฮคฮฟ ฯฮฑฯฮฑฯฮฌฮฝฯ applet Scratch ฮตฯฮนฯฯฮญฯฮตฮน ฯฮท ฮดฮนฮฑฮผฯฯฯฯฯฮท ฯฮฟฯ
ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ (x,t) ฮผฮต ฯฮท ฮฒฮฟฮฎฮธฮตฮนฮฑ ฯฮฟฯ
ฮดฮตฮฏฮบฯฮท ฯฮฟฯ
ฯฮฟฮฝฯฮนฮบฮนฮฟฯ: ฮบฮฌฮฝฮฟฮฝฯฮฑฯ ฮบฮปฮนฮบ ฮบฮฑฮน ฯฯฯฯฮนฮผฮฟ ฯฯฮฝ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฯฮฝยป – ฯฮฟฯ
ฮตฮฝฯฮฝฮฟฮฝฯฮฑฮน ฮผฮตฯฮฑฮพฯ ฯฮฟฯ
ฯ ฮผฮต ฮผฮนฮฑ ฮณฯฮฑฮผฮผฮฎ – ฯฯ
ฮฝฮนฯฯฮฟฯฮฝ ฯฮตฮปฮนฮบฮฌ ฮญฮฝฮฑ ฮณฯฮฌฯฮทฮผฮฑ (x,t) ฯฯฮฟ ฮฮฑฯฯฮตฯฮนฮฑฮฝฯ ฮฃฯฯฯฮทฮผฮฑ ฮฃฯ
ฮฝฯฮตฯฮฑฮณฮผฮญฮฝฯฮฝ. ฮฃฯฮท ฯฯ
ฮฝฮญฯฮตฮนฮฑ, ฮผฮต ฮบฮปฮนฮบ ฯฯฮฟ ฮบฮฟฯ
ฮผฯฮฏ ยซฮพฮตฮบฮฏฮฝฮฑยป ฯฮฑฯฮฑฮบฮฟฮปฮฟฯ
ฮธฮฟฯฮผฮต ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฯฮผฯฯฮฝฮฑ ฮผฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t). ฮฮฝฮดฮนฮฑฯฮญฯฮฟฮฝ ฯฮฑฯฮฟฯ
ฯฮนฮฌฮถฮตฮน ฮท ฮดฯ
ฮฝฮฑฯฯฯฮทฯฮฑ ฯฮฟฯ
ฯฯฮฟฯฯฮญฯฮตฮน ฯฮฟ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ: ฮผฯฮปฮนฯ ฮฟ ฮดฮตฮฏฮบฯฮทฯ ฯฮฟฯ
ฯฮฟฮฝฯฮนฮบฮนฮฟฯ ฮฑฮณฮณฮฏฮพฮตฮน ฮญฮฝฮฑ ฮฑฯฯ ฯฮฑ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฮฑยป ฯฮฟฯ
ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฮผฮฑฯ ฮญฮฝฮฑ ฮผฮฎฮฝฯ
ฮผฮฑ ฮผฮฑฯ ฯฮปฮทฯฮฟฯฮฟฯฮตฮฏ ฮณฮนฮฑ ฯฮนฯ ฮฑฮปฮณฮตฮฒฯฮนฮบฮญฯ ฯฮนฮผฮญฯ ฯฮทฯ ฮธฮญฯฮทฯ ฯฮฟฯ
ฮบฮนฮฝฮทฯฮฟฯ ฮบฮฑฮธฯฯ ฮบฮฑฮน ฯฮทฮฝ ฮฑฮฝฯฮฏฯฯฮฟฮนฯฮท ฯฯฮฟฮฝฮนฮบฮฎ ฯฯฮนฮณฮผฮฎ.
ฮโ ฮฑฯ
ฯฯฮฝ ฯฮฟฮฝ ฯฯฯฯฮฟ ฮตฯฮนฯฯ
ฮณฯฮฌฮฝฮตฯฮฑฮน ฮท ยซฮฑฮฝฮฌฮบฯฮนฯฮทยป ฯฯฮฝ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฯฮฝยป ฯฮฟฯ
ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฮบฮฑฮน ฮท ฯฯ
ฮฝฮฑฮณฯฮณฮฎ ฯฯ
ฮผฯฮตฯฮฑฯฮผฮฌฯฯฮฝ.ย
ฮฯฮนฯฮปฮญฮฟฮฝ, ฮฟฮน ฮฑฮปฮณฮตฮฒฯฮนฮบฮญฯ ฯฮนฮผฮญฯ ฯฮทฯ ฯฮฑฯฯฯฮทฯฮฑฯ ฯฮฟฯ
ฮบฮนฮฝฮทฯฮฟฯ ฮตฮผฯฮฑฮฝฮฏฮถฮฟฮฝฯฮฑฮน ฯฮต ฮผฮฟฮฝฮฟฮดฮนฮฌฯฯฮฑฯฮฟ ฯฮฏฮฝฮฑฮบฮฑ. ฮ ฯฯฮบฮตฮนฯฮฑฮน ฮณฮนฮฑ ฯฮนฮผฮญฯ ฯฮฟฯ
ฮฑฮฝฯฮนฯฯฮฟฮนฯฮฟฯฮฝ ฯฮต ฮบฮฑฮธฮญฮฝฮฑ ฮฑฯฯ ฯฮฑ ฮตฯฯฮฌ ฮตฯ
ฮธฯฮณฯฮฑฮผฮผฮฑ ฯฮผฮฎฮผฮฑฯฮฑ ฯฮฟฯ
ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฯฯฯฮต ฮฝฮฑ ฮตฮปฮญฮณฯฮตฯฮฑฮน ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฮบฮฑฯฮฌ ฯฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฯฮทฯ ฮดฮนฮฑฮผฯฯฯฯฯฮฎฯ ฯฮฟฯ
.
ฮฯฮฟฮฝ ฮฑฯฮฟฯฮฌ ฯฮทฮฝ ฯฮฑฯฮฑฮบฮฟฮปฮฟฯฮธฮทฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฮฟฯ
ฯฮฑฮนฮดฮนฮฟฯ ฯฯฮฟฮฝ ฮฌฮพฮฟฮฝฮฑ โ x, ฮผฮตฯฮฌ ฮฑฯฯ ฯฯฯฮปฮนฮฟ-ฯ
ฯฯฮดฮตฮนฮพฮท ฮตฮฝฯฯ ฮผฮฑฮธฮทฯฮฎ ฯฯฮฟ Scratch website, ฯฯฯฯฮธฮตฯฮฑ ฮผฮนฮฑ ฮบฮฑฯฮฑฮบฯฯฯ
ฯฮท ฯฯฮฌฯฮนฮฝฮท ฮณฯฮฑฮผฮผฮฎ ฯฮฟฯ
ฮผฮตฯฮฑฮบฮนฮฝฮตฮฏฯฮฑฮน ฯฯ
ฮฝฮตฯฯฯ ฮดฮตฮฏฯฮฝฮฟฮฝฯฮฑฯ ฯฮฟ ฮฑฮฝฯฮฏฯฯฮฟฮนฯฮฟ ฯฮทฮผฮตฮฏฮฟ ฯฮฟฯ
ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ. ฮ ฯฯฮบฮตฮนฯฮฑฮน ฮณฮนฮฑ ฮญฮฝฮฑ ฮตฮฝฮดฮนฮฑฯฮญฯฮฟฮฝ ฮฒฮฟฮทฮธฮทฯฮนฮบฯ ฮตฯฮณฮฑฮปฮตฮฏฮฟ ฮตฮปฮญฮณฯฮฟฯ
ฮผฮตฯฮฑฮพฯ ฮดฯฮฟ ฮฑฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฯฮฝ.
(A) ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฯฯ ฯฮท ฮปฮตฮบฯฮนฮบฮฎ ฯฮตฯฮนฮณฯฮฑฯฮฎ ฮบฮฏฮฝฮทฯฮทฯ ฮผฮนฮฑฯ ฮผฯฮฝฮฟ ฯฮฌฯฮทฯ ฯฯฮทฮฝ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮฏฮทฯฮท ฯฮทฯ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮฎ ฯฮทฯย
ฮฮฑฮธฯฯ ฮญฯฯฮนฮฑฯฮฝฮฑ ฯฮฟ project ฯฮบฮตฯฯฯฮผฮฟฯ
ฮฝฮฑ ฯฯฮน ฮฑฯ
ฯฯ ฮธฮฑ ฮตฮฏฮฝฮฑฮน ฯฯฮฎฯฮนฮผฮฟ ฮผฯฮฝฮฟ ฮณฮนฮฑ ฯฮทฮฝ ฮฑฯฮปฮฟฯฯฯฮตฯฮท ฯฯฮฝ ฮบฮนฮฝฮฎฯฮตฯฮฝ ฯฮฟฯ
ฮดฮนฮดฮฌฯฮบฮฟฯ
ฮผฮต ฯฯฮฟ ฯฯฮฟฮปฮตฮฏฮฟ ฮดฮทฮปฮฑฮดฮฎ ฯฮทฮฝ ยซฮฯ
ฮธฯฮณฯฮฑฮผฮผฮท ฮฮผฮฑฮปฮฎ ฮฮฏฮฝฮทฯฮทยป. ฮฃฯฮท ฯฯ
ฮฝฮญฯฮตฮนฮฑ ฮตฮฏฮดฮฑ ฯฯฮน ฮผฯฮฟฯฯ ฮฝฮฑ ฯฮฑฮฝฯฮฌฮถฮฟฮผฮฑฮน ฮบฮฑฮน ฮฝฮฑ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฯ ฮบฮฑฮน ฮฌฮปฮปฮตฯ ฮณฮฝฯฯฯฮญฯ ฮบฮนฮฝฮฎฯฮตฮนฯ ฮฑฮปฮปฮฌ ฮฑฯ
ฯฯ ฮผฯฮฝฮฟ ฮผฮต ฮผฮตฮณฮฌฮปฮท ฯฯฮฟฯฮญฮณฮณฮนฯฮท! ฮฯฯ ฯฮฟฮฝ ฯฯฯฯฮฟ ฯฮฟฯ
ฯฯฮฟฮณฯฮฑฮผฮผฮฑฯฮฏฯฯฮทฮบฮต ฯฮฟ applet ฮดฮตฮฝ ฮพฮตฯฮฝฮฌฯ ฯฯฮน ฯฮต ฮบฮฑฮธฮตฮผฮนฮฌ ฮฑฯฯ ฯฮนฯ ฮตฯฮนฮผฮญฯฮฟฯ
ฯ ฮตฯฯฮฌ ย ฯฮฌฯฮตฮนฯ ฮท ฯฮฑฯฯฯฮทฯฮฑ ฯฮฑฯฮฑฮผฮญฮฝฮท ฯฯฮฑฮธฮตฯฮฎ. ฮฯฮฝฮฟ ฮฑฮฝ ฮญฯฯฮนฮฑฯฮฝฮฑ ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t) ฯฯฮทฯฮนฮผฮฟฯฮฟฮนฯฮฝฯฮฑฯ ฮญฮฝฮฑ ฯฮฟฮปฯ ฮผฮตฮณฮฌฮปฮฟ ฯฮปฮฎฮธฮฟฯ ยซฯฮทฮผฮตฮฏฯฮฝยป ฮธฮฑ ฮบฮฑฯฮฌฯฮตฯฮฝฮฑ ฮฝฮฑ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮฎฯฯ ฯฮนฮฟ ฮนฮบฮฑฮฝฮฟฯฮฟฮนฮทฯฮนฮบฮฌ ฯฮนฯ ฮบฮนฮฝฮฎฯฮตฮนฯ.
A.1.ย [ฮฮตฮบฯฮนฮบฮฎ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท]ย ฮฆฮฑฮฝฯฮฑฮถฯฮผฮฑฯฯฮต ฯฮฟ ฯฮฑฮนฮดฮฏ ฮฝฮฑ ฮบฮนฮฝฮตฮฏฯฮฑฮน ฮตฯ
ฮธฯฮณฯฮฑฮผฮผฮฑ ฯฯฮฟ ฮดฯฯฮผฮฟ (ฮฌฮพฮฟฮฝฮฑฯโx) ฯฯฮฟฯ ฯฮฑ ฮดฮตฮพฮนฮฌ ฮผฮต ฯฯฮฑฮธฮตฯฮฎ ฯฮฑฯฯฯฮทฯฮฑ ฯ
=1 ฮผฮฟฮฝฮฌฮดฮฑ. ฮคฮท ฯฯฮฟฮฝฮนฮบฮฎ ฯฯฮนฮณฮผฮฎ t=0 ฯฮฟ ฯฮฑฮนฮดฮฏ ฯฮตฯฮฝฮฌฮตฮน ฮฑฯฯ ฯฮท ฮธฮญฯฮท x0=-83 pixels ฮบฮฑ ฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฮบฮฏฮฝฮทฯฮทฯ ฮตฮฏฮฝฮฑฮน 230 ฮผฮฟฮฝฮฌฮดฮตฯ ฯฯฯฮฝฮฟฯ
.
i) ฮฮต ฮบฮปฮนฮบ ฮบฮฑฮน ฯฯฯฯฮนฮผฮฟ ฯฯฮฑ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฮฑยป ฮดฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฯฮทฮฝ ฮฟฮธฯฮฝฮท ฯฮฟฯ
ฯ
ฯฮฟฮปฮฟฮณฮนฯฯฮฎ ฮญฯฯฮน ฯฯฯฮต ฮฝฮฑ ฯฮฑฯฮฑฮบฮฟฮปฮฟฯ
ฮธฮฎฯฮตฯฮต ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฮฟฯ
ฯฮฑฮนฮดฮนฮฟฯ.
ii) ฮฮฑฯฮนฮถฯฮผฮตฮฝฮฟฮน ฯฯฮนฯ ฯฮนฮผฮญฯ ฯฮฟฯ
ฮผฯฮฟฯฮตฮฏฯฮต ฮฝฮฑ ฮฑฮฝฯฮปฮฎฯฮตฯฮต ฮฑฯฯ ฯฮฑ ยซฯฮทฮผฮตฮฏฮฑยป ฯฮฟฯ
ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ — ฮฝฮฑ ฯ
ฯฮฟฮปฮฟฮณฮฏฯฮตฯฮต ฯฮท ฮผฮตฯฮฑฯฯฯฮนฯฮท ฯฮฟฯ
ฯฮฑฮนฮดฮนฮฟฯ ฮบฮฑฯฮฌ ฯฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฯฯฮฝ 230 ฮผฮฟฮฝฮฌฮดฯฮฝ ฯฯฯฮฝฮฟฯ
. —ฮฝฮฑ ฮฑฯฮฟฮดฮตฮฏฮพฮตฯฮต ฯฯฮน ฮท ฮบฮปฮฏฯฮท ฯฮฟฯ
ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฯฯ ฯฯฮฟฯ ฯฮฟฮฝ ฮฌฮพฮฟฮฝฮฑ โt ฮตฮฏฮฝฮฑฮน 45 ฮผฮฟฮฏฯฮตฯ.
iii) ฮฮฑ ฮฒฯฮตฮฏฯฮต ฯฮทฮฝ ฮตฮพฮฏฯฯฯฮท ฮบฮฏฮฝฮทฯฮทฯ ฮณฮนฮฑ ฯฮท ฮธฮญฯฮท ฯฮฟฯ
ฮบฮนฮฝฮทฯฮฟฯ

ฮ.2. [ฮฮตฮบฯฮนฮบฮฎ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท]ย ฮฆฮฑฮฝฯฮฑฮถฯฮผฮฑฯฯฮต ฯฮฟ ฯฮฑฮนฮดฮฏ ฮฝฮฑ ฮบฮนฮฝฮตฮฏฯฮฑฮน ฮตฯ
ฮธฯฮณฯฮฑฮผฮผฮฑ ฮผฮต ฯฮฑฯฯฯฮทฯฮฑ ฯ
=-0.5 ฮผฮฟฮฝฮฌฮดฮตฯ. ฮคฮท ฯฯฮนฮณฮผฮฎ t=0 ฯฮฟ ฯฮฑฮนฮดฮฏ ฮดฮนฮญฯฯฮตฯฮฑฮน ฮฑฯฯ ฯฮทฮฝ ฮฑฯฯฮฎ ฯฮฟฯ
ฮฌฮพฮฟฮฝฮฑ โx ฮบฮฑฮน ฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฮบฮฏฮฝฮทฯฮทฯ ฮตฮฏฮฝฮฑฮน 230 ฮผฮฟฮฝฮฌฮดฮตฯ ฯฯฯฮฝฮฟฯ
.
i) ฮฮต ฮบฮปฮนฮบ ฮบฮฑฮน ฯฯฯฯฮนฮผฮฟ ฯฯฮฑ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฮฑยป ฮดฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฯฮทฮฝ ฮฟฮธฯฮฝฮท ฯฮฟฯ
ฯ
ฯฮฟฮปฮฟฮณฮนฯฯฮฎ ฮญฯฯฮน ฯฯฯฮต ฮฝฮฑ ฯฮฑฯฮฑฮบฮฟฮปฮฟฯ
ฮธฮฎฯฮตฯฮต ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฮฟฯ
ฯฮฑฮนฮดฮนฮฟฯ.
ii) ฮฮฑฯฮนฮถฯฮผฮตฮฝฮฟฮน ฯฯฮนฯ ฯฮนฮผฮญฯ ฯฮฟฯ
ฮผฯฮฟฯฮตฮฏฯฮต ฮฝฮฑ ฮฑฮฝฯฮปฮฎฯฮตฯฮต ฮฑฯฯ ฯฮฑ ยซฯฮทฮผฮตฮฏฮฑยป ฯฮฟฯ
ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ
— ฮฝฮฑ ฯ
ฯฮฟฮปฮฟฮณฮฏฯฮตฯฮต ฯฮท ฮผฮตฯฮฑฯฯฯฮนฯฮท ฯฮฟฯ
ฯฮฑฮนฮดฮนฮฟฯ ฮบฮฑฯฮฌ ฯฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฯฯฮฝ 230 ฮผฮฟฮฝฮฌฮดฯฮฝ ฯฯฯฮฝฮฟฯ
—ฮฝฮฑ ฯ
ฯฮฟฮปฮฟฮณฮฏฯฮตฯฮต ฯฮทฮฝ ฮบฮปฮฏฯฮท ฯฮฟฯ
ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฯฯ ฯฯฮฟฯ ฯฮฟฮฝ ฮฌฮพฮฟฮฝฮฑ โt.
iii) ฮฮฑ ฮฒฯฮตฮฏฯฮต ฯฮทฮฝ ฮตฮพฮฏฯฯฯฮท ฮบฮฏฮฝฮทฯฮทฯ ฮณฮนฮฑ ฯฮท ฮธฮญฯฮท ฯฮฟฯ
ฮบฮนฮฝฮทฯฮฟฯ
 (B) ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฯฯ ฯฮทฮฝ ฮฑฮปฮณฮตฮฒฯฮนฮบฮฎ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท ฮผฮนฮฑฯ ฮตฯ
ฮธฯฮณฯฮฑฮผฮผฮทฯ ฮฟฮผฮฑฮปฮฎฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฯฮทฮฝ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮฏฮทฯฮท ฯฮทฯ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮฎฯ ฯฮทฯ
(B) ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฯฯ ฯฮทฮฝ ฮฑฮปฮณฮตฮฒฯฮนฮบฮฎ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท ฮผฮนฮฑฯ ฮตฯ
ฮธฯฮณฯฮฑฮผฮผฮทฯ ฮฟฮผฮฑฮปฮฎฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฯฮทฮฝ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮฏฮทฯฮท ฯฮทฯ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮฎฯ ฯฮทฯ
B.1. ฮ ฮตฮพฮฏฯฯฯฮท ฮบฮฏฮฝฮทฯฮทฯ ฮณฮนฮฑ ฯฮท ฮธฮญฯฮท ฯฮฟฯ
ฯฮฑฮนฮดฮนฮฟฯ [ฮฑฮปฮณฮตฮฒฯฮนฮบฮฎ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท] ฮตฮฏฮฝฮฑฮนย x(t) = 100 – t ฮบฮฑฮน ฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฯฮทฯ ฮตฮฏฮฝฮฑฮน 200 ฮผฮฟฮฝฮฌฮดฮตฯ ฯฯฯฮฝฮฟฯ
.
i) ฮ ฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮฎฯฯฮต ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ
ii) ฮงฯฮทฯฮนฮผฮฟฯฮฟฮนฯฮฝฯฮฑฯ ฯฮทฮฝ ฮตฮพฮฏฯฯฯฮท ฮบฮฏฮฝฮทฯฮทฯ ฯ
ฯฮฟฮปฮฟฮณฮฏฯฯฮต ฯฮท ฮธฮญฯฮท ฯฮฟฯ
ฯฮฑฮนฮดฮนฮฟฯ ฯฮท ฯฯฮฟฮฝฮนฮบฮฎ ฯฯฮนฮณฮผฮฎ t=200 ฮผฮฟฮฝฮฌฮดฮตฯ ฯฯฯฮฝฮฟฯ
.
iii) ฮฯฮนฮฒฮตฮฒฮฑฮนฯฯฯฮต ฯฮทฮฝ ฮฟฯฮธฯฯฮทฯฮฑ ฯฮทฯ ฮฑฯฮฌฮฝฯฮทฯฮทฯ ฮฑฯฯ ฯฮนฯ ฯฮปฮทฯฮฟฯฮฟฯฮฏฮตฯ ฯฮฟฯ
ฯฮฑฯ ฯฮฑฯฮญฯฮตฮน ฯฮฟ applet.

(ฮ) ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฮท ฮฟฮผฮฑฮปฮฌ ฮผฮตฯฮฑฮฒฮฑฮปฮปฯฮผฮตฮฝฮตฯ ฮบฮนฮฝฮฎฯฮตฮนฯ
ฮฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฯฯฮต ฮท ฮบฮฏฮฝฮทฯฮท ฯฮฟฯ
ฯฮฑฮนฮดฮนฮฟฯ ฯฯฮฟฮฝ ฮฌฮพฮฟฮฝฮฑ x:
ฮ.1.ฮฮฑ ฮตฮฏฮฝฮฑฮน ฮฑฯ
ฮพฮฑฮฝฯฮผฮตฮฝฮทฯ ฯฮฑฯฯฯฮทฯฮฑฯ ฮบฮฑฯฮฌ ฯฯฮฟฮฝฮนฮบฮฌ ฮดฮนฮฑฯฯฮฎฮผฮฑฯฮฑ

ฮ.2. ฮฮฑ ฮตฮฏฮฝฮฑฮน ฮตฮปฮฑฯฯฮฟฯฮผฮตฮฝฮทฯ ฯฮฑฯฯฯฮทฯฮฑฯ

ฮ.3. ฮฮฑ ฮตฮฏฮฝฮฑฮน ฮฑฯ
ฮพฮฑฮฝฯฮผฮตฮฝฮท ฮผฮญฯฯฮน ฯฮทฮฝ ฮฑฯฯฮฎ ฯฮฟฯ
ฮฌฮพฮฟฮฝฮฑ ฮบฮฑฮน ฯฯฮท ฯฯ
ฮฝฮญฯฮตฮนฮฑ ฮตฮปฮฑฯฯฮฟฯฮผฮตฮฝฮท.

ฮ.4. ฮฮฑ ยซฮผฮฟฮนฮฌฮถฮตฮนยป ฮผฮต ฮฑฯ
ฯฮฎฮฝ ฯฮทฯ ฯฮฑฮปฮฌฮฝฯฯฯฮทฯ ฮผฮนฮฑฯ ฯฮตฯฮนฯฮดฮฟฯ
.

ฮ. ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฯฮฌฯฮทฮผฮฑ (x,t) ฮผฮต ฮดฮนฮฑฮบฯฮนฯฮญฯ ฯฮฌฯฮตฮนฯ (ฮผฮต ฯ
=ฯฯฮฑฮธฮตฯฯ, ฯ
=0)
ฮ.1.ย ฮคฮท ฯฯฮฟฮฝฮนฮบฮฎ ฯฯฮนฮณฮผฮฎ t=0 ฯฮฟ ฯฮฑฮนฮดฮฏ ฯฮตฯฮฝฮฌฮตฮน ฮฑฯฯ ฯฮทฮฝ ฮฑฯฯฮฎ ฯฮฟฯ
ฯฯฮฟฯฮฑฮฝฮฑฯฮฟฮปฮนฯฮผฮญฮฝฮฟฯ
ฮฌฮพฮฟฮฝฮฑ ฮบฮฑฮน ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮตฮฏ ฮตฯ
ฮธฯฮณฯฮฑฮผฮผฮท ฮฟฮผฮฑฮปฮฎ ฮบฮฏฮฝฮทฯฮท ฯฯฮฟฯ ฯฮฑ ฮดฮตฮพฮนฮฌ ฮบฮฑฮน ฯฯฮท ฯฯ
ฮฝฮญฯฮตฮนฮฑ ฯฮฑฯฮฑฮผฮญฮฝฮตฮน ฮฑฮบฮฏฮฝฮทฯฮฟ ฮณฮนฮฑ ฯฯฯฮฝฮฟ 30 ฮผฮฟฮฝฮฌฮดฯฮฝ. ฮฮตฯฮฌ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮตฮฏ ฮบฮฏฮฝฮทฯฮท ฮผฮต ฯฯฮฑฮธฮตฯฮฎ ฯฮฑฯฯฯฮทฯฮฑ ฮบฮฑฮน ฯฮตฮปฮตฮนฯฮฝฮตฮน ฮผฯฮปฮนฯ ฯฮฟ ฯฮฑฮนฮดฮฏ ฮตฯฮนฯฯฯฮญฯฮตฮน ฯฯฮทฮฝ ฯฯฮทฮฝ ฮฑฯฯฮฎ ฯฮฟฯ
ฮฌฮพฮฟฮฝฮฑ x.ย
i) ฮฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฮฟฯ
ฮฑฮฝฯฮนฯฯฮฟฮนฯฮตฮฏ ฯฯฮท ฮปฮตฮบฯฮนฮบฮฎ ฯฮตฯฮนฮณฯฮฑฯฮฎ.
ii) ยซฮคฯฮญฮพฯฮตยป ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฮผฮต ฯฮบฮฟฯฯ ฮฝฮฑ ฮฒฮตฮฒฮฑฮนฯฮธฮตฮฏฯฮต ฮณฮนฮฑ ฯฮทฮฝ ฮฟฯฮธฯฯฮทฯฮฑ ฯฮทฯ ฮปฮตฮบฯฮนฮบฮฎฯ ฯฮตฯฮนฮณฯฮฑฯฮฎฯ.

ฮ. ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฯฯ ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t) ฯฯฮท ฮปฮตฮบฯฮนฮบฮฎ ฯฮตฯฮนฮณฯฮฑฯฮฎ ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ
ฮ.1. ฮฮฏฮฝฮตฯฮฑฮน ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ:
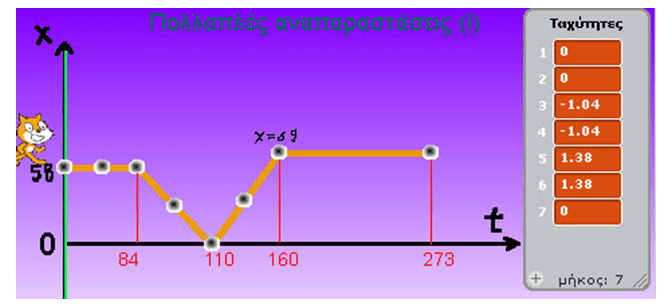
- i) ฮฮฑ ฯฮตฯฮนฮณฯฮฌฯฮตฯฮต ฯฮทฮฝ ฮบฮฏฮฝฮทฯฮท ฯฮฟฯ
ฯฮฑฮนฮดฮนฮฟฯ ฯฯฮผฯฯฮฝฮฑ ฮผฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ
ii) ฮ ฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮฎฯฯฮต ฯฮนฯ ฯฯฮฟฯฮฟฮผฮฟฮนฯฯฮตฮนฯ ฮผฮต ฮฒฮฌฯฮท ฯฮฑ ฮณฯฮฑฯฮฎฮผฮฑฯฮฑ ฮบฮฑฮน ฮตฯฮนฮฒฮตฮฒฮฑฮนฯฯฯฮต ฯฮทฮฝ ฮฟฯฮธฯฯฮทฯฮฑ ฯฯฮฝ ฮปฮตฮบฯฮนฮบฯฮฝ ฯฮตฯฮนฮณฯฮฑฯฯฮฝ.
iii) ฮฅฯฮฟฮปฮฟฮณฮฏฯฯฮต ฯฮฑฯฯฯฮทฯฮตฯ, ฮผฮตฯฮฑฯฮฟฯฮฏฯฮตฮนฯ ฮบฮฑฮน ฯฯฮฟฮฝฮนฮบฮญฯ ฮดฮนฮฌฯฮบฮตฮนฮตฯ ฮผฮต ฮฒฮฌฯฮท ฯฮนฯ ฯฮปฮทฯฮฟฯฮฟฯฮฏฮตฯ ฯฮฟฯ
ฮดฮฏฮฝฮฟฮฝฯฮฑฮน ฯฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ.
ฮ. ฮฮฏฮฝฮฟฮฝฯฮฑฮน ฮดฯฮฟ ฮณฯฮฑฯฮนฮบฮญฯ ฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯ (ฮธฮญฯฮทฯ, ฯฯฯฮฝฮฟฯ
) ฯฯฮฟ ฮฏฮดฮนฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฮฟฯ
ฮฑฮฝฮฑฯฮญฯฮฟฮฝฯฮฑฮน ฯฯฮทฮฝ ฮบฮฏฮฝฮทฯฮท ฮตฮฝฯฯ ฮบฮฟฯฮนฯฯฮนฮฟฯ ฮบฮฑฮน ฮตฮฝฯฯ ฮฑฮณฮฟฯฮนฮฟฯ ฮฑฮฝฯฮฏฯฯฮฟฮนฯฮฑ.
ฮ.1.ฮฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฑ ฮดฮนฮบฮฌ ฯฮฑฯ ฮตฯฯฯฮฎฮผฮฑฯฮฑ ฯฮฟฯ
ฮท ฮฑฯฮฌฮฝฯฮทฯฮฎ ฯฮฟฯ
ฯ ฮตฯฮนฮฒฮฌฮปฮปฮตฮน ฯฮท ฮดฮนฮฑฮผฯฯฯฯฯฮท ฯฯฮฝ ฮดฯฮฟ ฮณฯฮฑฯฮนฮบฯฮฝ ฯฮฑฯฮฑฯฯฮฌฯฮตฯฮฝ (ฮณฮนฮฑ ฯฮฑฯฮฌฮดฮตฮนฮณฮผฮฑ, ฯฮฑ ฯฮฑฮนฮดฮนฮฌ ฮฝฮฑ ฯฯ
ฮฝฮฑฮฝฯฮนฮฟฯฮฝฯฮฑฮน ฯฯฮตฮนฯ ฯฮฟฯฮญฯ, ฮฝฮฑ ฮบฮนฮฝฮฟฯฮฝฯฮฑฮน ฮตฯ
ฮธฯฮณฯฮฑฮผฮผฮฑ ฮบฮฑฮน ฮฟฮผฮฑฮปฮฌ ฮบ.ฮป.ฯ.).
ฮ.2. โฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆ.
(Tฮฟ project ฮฑฮฝฮฑฯฯฮฎฮธฮทฮบฮต ฯฯฮทฮฝ ฮฮฟฮนฮฝฯฯฮทฯฮฑ ฯฮฟฯ
Scratch ฯฮฟ ฮฮฟฮญฮผฮฒฯฮท ฯฮฟฯ
2013 https://scratch.mit.edu/projects/13973896/ )

ฮฃฮทฮผฮตฮฏฯฯฮท 1. ฮฮน ฮญฮพฮน ฯฯฮฟฯฮตฮนฮฝฯฮผฮตฮฝฮตฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮตฯ ฮดฯฮฑฯฯฮทฯฮนฮฟฯฮฎฯฯฮฝ ฯฯ
ฮฝฮฟฮดฮตฯฮฟฮฝฯฮฑฮน ฮฑฯฯ ฯฮนฯ ฯฮตฮปฮฏฮดฮตฯ ฮฟฮธฯฮฝฮทฯ ฯฮฟฯ
ยซฮญฯฯฯฮฑยป ฮบฮฑฮธฯฯ ฮดฮนฮฑฮผฯฯฯฯฮฝฮฑ ฯฮนฯ ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮบฮฑฮน ฮตฮฏฮฝฮฑฮน ฮตฮฝฮดฮตฮนฮบฯฮนฮบฮญฯ. ฮคฮตฮปฮตฮนฯฮฝฮฟฮฝฯฮฑฯ ฮฑฯ
ฯฮฎ ฯฮทฮฝ ฮตฯฮณฮฑฯฮฏฮฑ ฮดฮนฮฑฯฮฏฯฯฯฯฮฑ ฯฮฟฮฝ ฯฮปฮฟฯฯฮฟ ฯฯฮฝ ฮดฯ
ฮฝฮฑฯฮฟฯฮฎฯฯฮฝ ฯฮฟฯ
ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฯฯฮฟฯฯฮญฯฮฟฯ
ฮฝ ฮดฯฮฟ ฯฯฯฮฟ ฮผฮนฮบฯฮฌ ฮตฮพฮตฮนฮดฮนฮบฮตฯ
ฮผฮญฮฝฮฑ applets Scratchโฆ
ฮฃฮทฮผฮตฮฏฯฯฮท 2. ฮฯฮฟฮนฮฟฯ ฮตฮฝฮดฮนฮฑฯฮญฯฮตฯฮฑฮน ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฮดฮตฮน ฯฮฟฮฝ ฮบฯฮดฮนฮบฮฑ ฯฯฮฟฮณฯฮฑฮผฮผฮฑฯฮนฯฮผฮฟฯ ฮตฮฝฯฯ Scratch project ฮบฮฑฯฮตฮฒฮฌฮถฮฟฮฝฯฮฑฯ ฯฮฟ ฮฑฯฯฮตฮฏฮฟ ฮฑฯฯ ฯฮฟ Scratch Website ฮฑฯฮฟฯ ฯฯฯฯฮฑ ฮญฯฮตฮน ฮบฮฑฯฮตฮฒฮฌฯฮตฮน ฯฯฮฟฮฝ ฯ
ฯฮฟฮปฮฟฮณฮนฯฯฮฎ ฯฮฟฯ
ฯฮฟ ฮตฮปฮตฯฮธฮตฯฮฟ ฮปฮฟฮณฮนฯฮผฮนฮบฯ ฮฑฯฯ ฯฮฟย http://www.scratch.mit.edu/ย ย ย . ฮฃฯฮท ฯฯ
ฮฝฮญฯฮตฮนฮฑ ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฯฮฟ ฯฯฮญฮพฮตฮน ฯฮต ฮฟฮปฯฮบฮปฮทฯฮท ฯฮทฮฝ ฮฟฮธฯฮฝฮท ฮผฮต ฮบฮปฮนฮบ ฯฯฮฟ ฮบฮฟฯ
ฮผฯฮฏ ฮ ฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ ฮ ฮฑฯฮฟฯ
ฯฮฏฮฑฯฮทฯ ฯฮฟฯ
ฮฒฯฮฏฯฮบฮตฯฮฑฮน ฯฯฮฟ ฯฮฌฮฝฯ ฮดฮตฮพฮฏ ฮผฮญฯฮฟฯ ฯฮทฯ ฮฟฮธฯฮฝฮทฯ ฮฎ ฮฝฮฑ ฯฮฟ ฮฑฮพฮนฮฟฯฮฟฮนฮฎฯฮตฮน ฮผฮต ฮฒฮนฮฝฯฮตฮฟฯฯฮฟฮฒฮฟฮปฮญฮฑ ฮฎ ฮดฮนฮฑฮดฯฮฑฯฯฮนฮบฯ ฯฮฏฮฝฮฑฮบฮฑ (ฮตฯฯฯฮฟฮฝ ฮตฮฝฮดฮตฮฏฮบฮฝฯ
ฯฮฑฮน).
ฮฮฟฮนฮฝฮฟฯฮฟฮนฮฎฯฯฮต:
ฮฃฯฮตฯฮนฮบฮฌ




ฮฃฮตฯ 12 2017
ฮฯฮนฮฝฯฮทฯฮท ฮดฯฮฑฯฯฮทฯฮนฮฟฯฮฎฯฯฮฝ ยซฮ ฮฟฮปฮปฮฑฯฮปฯฮฝ ฮฑฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฯฮฝยป ฮผฮต applets ฮฮนฮฝฮทฮผฮฑฯฮนฮบฮฎฯ: ฮคฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t)
ฮคฮฟฯ ฮฮฏฮบฮฟฯ ฮฮฑฯฯฮฝฯฮต
ยซฮ ฯฮนฮฝ ฮฑฯโ ฯฮปฮฑ ฯฯฮญฯฮตฮน ฮฝฮฑ ฮดฮนฮฑฯฯ ฯฯฮฝฮฟฯ ฮผฮต ฯฮฑ ฯฯฮฟฮฒฮปฮฎฮผฮฑฯฮฑ.ย ฮฮฑฮน ฯฮฑฯฮฌ ฯฮฑ ฮปฮตฮณฯฮผฮตฮฝฮฑ, ฯฯฮทฮฝ ฮตฯฮนฯฯฮทฮผฮฟฮฝฮนฮบฮฎ ฮถฯฮฎ ฯฮฑ ฯฯฮฟฮฒฮปฮฎฮผฮฑฯฮฑ ฮดฮตฮฝ ฯฮฏฮธฮตฯฮฑฮน ฮฑฯฯ ฮผฯฮฝฮฑ ฯฮฟฯ ฯ. ฮฮนฮฑ ฯฮฟ ฮตฯฮนฯฯฮทฮผฮฟฮฝฮนฮบฯ ฯฮฝฮตฯฮผฮฑ ฮบฮฌฮธฮต ฮณฮฝฯฯฮท ฮตฮฏฮฝฮฑฮน ฮฑฯฮฌฮฝฯฮทฯฮท ฯฮต ฮผฮนฮฑ ฮตฯฯฯฮทฯฮท. ฮฮฝ ฮดฮตฮฝ ฯ ฯฮฎฯฮพฮต ฮตฯฯฯฮทฮผฮฑ ฮดฮตฮฝ ฯ ฯฮฌฯฯฮตฮน ฮตฯฮนฯฯฮทฮผฮฟฮฝฮนฮบฮฎ ฮณฮฝฯฯฮท.ย
ย ย ย ย ย ย ย ย ย ฮคฮฏฯฮฟฯฮฑ ฮดฮตฮฝ ฮตฮฏฮฝฮฑฮน ฮฑฯ ฯฮฟฮฝฯฮทฯฮฟ. ฮคฮฑ ฯฮฌฮฝฯฮฑ ฮฟฮนฮบฮฟฮดฮฟฮผฮฟฯฮฝฯฮฑฮนยป
ฮฯฯฯฯฮฑฯฮผฮฑ ฮฑฯฯ ฯฮฟ ฮฒฮนฮฒฮปฮฏฮฟย ยซฮ ฮดฮนฮฑฮผฯฯฯฯฯฮท ฯฮฟฯ ฮตฯฮนฯฯฮทฮผฮฟฮฝฮนฮบฮฟฯ ฯฮฝฮตฯฮผฮฑฯฮฟฯยปย ฯฮฟฯ ฮฮฌฮปฮปฮฟฯ ฮตฯฮนฯฯฮฎฮผฮฟฮฝฮฑ ฮบฮฑฮน ฯฮนฮปฮฟฯฯฯฮฟฯ Gaston Bachelard
ฮฮนฯฮฑฮณฯฮณฮฎ
ฮฮน ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮฟฯ ฮดฮฏฮฝฮฟฮฝฯฮฑฮน ฯฯฮฟฯ ฯ ฮผฮฑฮธฮทฯฮญฯ ฮฮฮฯ ฮบฮตฮฏฮฟฯ ฮผฮต ฮธฮญฮผฮฑ ฯฮนฯ ฮณฯฮฑฯฮนฮบฮญฯ ฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯ ฯฯฮฟฮฝ ฯฮฟฮผฮญฮฑ ฯฮทฯ ฮฮนฮฝฮทฮผฮฑฯฮนฮบฮฎฯ, ฯฮฑฯฮฑฮผฮญฮฝฮฟฯ ฮฝ ฯฯฮตฮดฯฮฝ ฮฑฮฝฮฑฮปฮปฮฟฮฏฯฯฮตฯ ฮตฮดฯ ฮบฮฑฮน ฯฮฟฮปฮปฮฌ ฯฯฯฮฝฮนฮฑ. ฮคฮฟ ฮฏฮดฮนฮฟ ฮฑฮบฯฮนฮฒฯฯ ฯฯ ฮผฮฒฮฑฮฏฮฝฮตฮน ฮบฮฑฮน ฮผฮต ฯฮนฯ ฮตฯฮนฮดฮนฯฮบฯฮผฮตฮฝฮตฯ ฮนฮบฮฑฮฝฯฯฮทฯฮตฯ ฯฮฟฯ ฯฯฮฟฯฮดฮฟฮบฮฟฯฮผฮต ฮฝฮฑ ฮฑฯฮฟฮบฯฮฎฯฮฟฯ ฮฝ ฮฟฮน ฮผฮฑฮธฮทฯฮญฯ.
ฮฮฑฯฮฌ ฯฮท ฮณฮฝฯฮผฮท ฮผฮฟฯ , ฮฑฯ ฯฯ ฮฟฯฮตฮฏฮปฮตฯฮฑฮน ฯฮต ฮผฮตฮณฮฌฮปฮฟ ฮฒฮฑฮธฮผฯ ฮบฮฑฮน ฯฯฮฟ ฮณฮตฮณฮฟฮฝฯฯ ฯฯฮน ฯฯฮท ฮดฮนฮดฮฑฯฮบฮฑฮปฮฏฮฑ ฮผฮฑฯ, ฯฯฯฯ ฮบฮฑฮน ฯฯฮนฯ ฮตฮพฮตฯฮฌฯฮตฮนฯ, ฮฟฮน ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮฒฮฑฯฮฏฮถฮฟฮฝฯฮฑฮน ฯฯฮฑ ฮผฮญฯฮฑ ฯฮฟฯ ฮบฯ ฯฮฏฯฯ ฯฯฮทฯฮนฮผฮฟฯฮฟฮนฮฟฯฮผฮต: ฯฮฟฮฝ ฮบฮนฮผฯฮปฮนฮฟฯฮฏฮฝฮฑฮบฮฑ, ฯฮฟ ฯฯฮฟฮปฮนฮบฯ ฮตฮณฯฮตฮนฯฮฏฮดฮนฮฟ ฮบฮฑฮน ฯฮฟ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ ยซฯฮฑฯฯฮฏ-ฮผฮฟฮปฯฮฒฮนยป.
ฮฮฝ ฮตฯฮนฮธฯ ฮผฮฟฯฮผฮต ฯฮทฮฝ ฮฑฮฝฮฑฮฝฮญฯฯฮท ฯฮฟฯ ฯฮตฯฮตฯฯฮฟฯฮฏฮฟฯ ฯฯฮฝ ฮดฯฮฑฯฯฮทฯฮนฮฟฯฮฎฯฯฮฝ ฮบฮฑฮน ฯฯฮฝ ฯฯฯฯฯฮฝ ฮดฮนฮดฮฑฯฮบฮฑฮปฮฏฮฑฯ ฮผฮฑฯ ฮดฮตฮฝ ฮญฯฮฟฯ ฮผฮต ฯฮฑฯฮฌ ฮฝฮฑ ฯฯฯฮญฯฮฟฯ ฮผฮต ฯฮฟ ฮตฮฝฮดฮนฮฑฯฮญฯฮฟฮฝ ฮผฮฑฯ ฯฮต ยซฮผฮนฮบฯฮฌ ฮตฮพฮตฮนฮดฮนฮบฮตฯ ฮผฮญฮฝฮฑ ฮผฮนฮบฯฮฌ ฯฯฮฟฮณฯฮฌฮผฮผฮฑฯฮฑยป (applets Scratch) ฯฮฟฯ ฯฯฮญฯฮฟฯ ฮฝ ฮฑฯฮตฯ ฮธฮตฮฏฮฑฯ ฯฯฮฟ ฮดฮนฮฑฮดฮฏฮบฯฯ ฮฟ ฮบฮฑฮน ฮฒฮญฮฒฮฑฮนฮฑ ฮผฯฮฟฯฮฟฯฮฝ ฮฝฮฑ ฯฯฮญฮพฮฟฯ ฮฝ “ฮฑฯ ฯฯฮฝฮฟฮผฮฑ” ฯฯฮฟฮฝ ฯ ฯฮฟฮปฮฟฮณฮนฯฯฮฎ ฮผฮฑฯ. ฮฯฯฮน, ฮตฯฮนฯฯ ฮณฯฮฌฮฝฮตฯฮฑฮน ฯฮฟ ฮผฮตฮณฮฑฮปฯฯฮตฯฮฟ ฮตฯฯฮฟฯ ฯฯฮฝ ฯฯฮฟฯฯฮตฯฮฟฮผฮญฮฝฯฮฝ ฮดฯ ฮฝฮฑฯฮฟฯฮฎฯฯฮฝ: ฮดฮนฮฑฮดฮฏฮบฯฯ ฮฟ, ฮฒฮนฮฝฯฮตฮฟฯฯฮฟฮฒฮฟฮปฮญฮฑฯ ฮบฮฑฮน ฮดฮนฮฑฮดฯฮฑฯฯฮนฮบฯฯ ฯฮฏฮฝฮฑฮบฮฑฯ ฯฯฮท ฯฯฮฟฮปฮนฮบฮฎ ฯฮฌฮพฮท ฮฎ ฯฯฮฟ ฮตฯฮณฮฑฯฯฮฎฯฮนฮฟ ฯ ฯฮฟฮปฮฟฮณฮนฯฯฯฮฝ.
ฮฮผฯฯ, ฮท ฮตฯฮนฮฝฯฮทฯฮท ฮฝฮญฯฮฝ ฮดฯฮฑฯฯฮทฯฮนฮฟฯฮฎฯฯฮฝ ฯฮฟฯ ฮฝฮฑ ฮฒฮฑฯฮฏฮถฮฟฮฝฯฮฑฮน ฯโ ฮฑฯ ฯฮฌ ฯฮฑ applets ฮดฮตฮฝ ฮตฮฏฮฝฮฑฮน ฮตฯฮบฮฟฮปฮท ฯ ฯฯฮธฮตฯฮท. ฮฮนฮฑ ฯฮทฮฝ ฮตฯฮนฮฝฯฮทฯฮฎ ฯฮฟฯ ฯ ฮฑฯฮฑฮนฯฮตฮฏฯฮฑฮน ฯฯฯฮฟ ฮท ฯฯ ฮฝฮตฯฮณฮฑฯฮฏฮฑ ฯฯฮฝ ฮตฮบฯฮฑฮนฮดฮตฯ ฯฮนฮบฯฮฝ ฯฮทฯ ฯฯฮฌฮพฮทฯ ฯฯฮฟ ฮบฮฑฮน ฮท ฮดฮฟฮบฮนฮผฮฑฯฮฏฮฑ ฯฮฟฯ ฯ ฯฯฮทฮฝ ฯฯฮฑฮณฮผฮฑฯฮนฮบฮฎ ฯฯฮฟฮปฮนฮบฮฎ ฯฮฌฮพฮท. ฮฮฑฮถฮฏ ฮผฮต ฮฑฯ ฯฮฌ, ฯฮทฮผฮฑฮฝฯฮนฮบฯ ฮตฮฏฮฝฮฑฮน ฮบฮฑฮน ฯฮฟ ฮฝฮฑ ยซฮผฮฟฮนฯฮฑฮถฯฮผฮฑฯฯฮตยป ฯฮนฯ ฮนฮดฮญฮตฯ ฮบฮฑฮน ฯฮนฯ ฯฯฮฟฯฮฌฯฮตฮนฯ ฮผฮฑฯ ฮผฮฑฮถฮฏ ฮผฮต ฮฌฮปฮปฮฟฯ ฯ ฮตฮบฯฮฑฮนฮดฮตฯ ฯฮนฮบฮฟฯฯ ฯฯ ฮผฮผฮตฯฮญฯฮฟฮฝฯฮฑฯ ฯฯฮนฯ ฮผฮนฮบฯฮญฯ ฮฎ ฮผฮตฮณฮฌฮปฮตฯ ยซฮฮฟฮนฮฝฯฯฮทฯฮตฯยป ฯฮฟฯ ฮตฮผฯฮฑฮฝฮฏฮถฮฟฮฝฯฮฑฮน ฯฯฮฟฮฝ ฮบฯ ฮฒฮตฯฮฝฮฟฯฯฯฮฟ.
ฮ ฮฒฮฑฯฮนฮบฮฎ ฯ ฯฯฮธฮตฯฮท ฯฮฟฯ ฯ ฯฮฟฯฯฮทฯฮฏฮถฯ ฮดฮตฮฝ ฮตฮฏฮฝฮฑฮน ฮฌฮปฮปฮท ฮฑฯฯ ฮผฮตฯฮนฮบฮญฯ ฮนฮดฮญฮตฯ ฯฮฟฯ ฮญฯฮฟฯ ฮฝ ฮดฮนฮฑฯฯ ฯฯฮธฮตฮฏ ฮฑฮฝฮฑฯฮฟฯฮนฮบฮฌ ฮผฮต ฯฮนฯ ยซฮ ฮฟฮปฮปฮฑฯฮปฮญฯ ฮฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯยป. ฮฯ ฯฮฏฮฑฯฯฮท ฮธฮตฯฯฯ ฯฮทฮฝ ฮนฮดฮญฮฑ ฯฯฮน ฮท ฮผฮฌฮธฮทฯฮท ฮดฮนฮตฯ ฮบฮฟฮปฯฮฝฮตฯฮฑฮน ฮฑฮฝ ฮฟฮน ฮผฮฑฮธฮทฯฮญฯ ฮฑฯฮบฮฟฯฮฝฯฮฑฮน ฮผฮต ฮผฮตฯฮฑฮฒฮฌฯฮตฮนฯ ฮฑฯฯ ฯฮท ฮผฮนฮฑ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท ฯฯฮทฮฝ ฮฌฮปฮปฮท ฮฟฯฯฯฮต ฮญฯฯฮน ฮตฮฝฮนฯฯฯฮตฯฮฑฮน ฮบฮฑฮน ฮท ฮฟฮนฮบฮฟฮดฯฮผฮทฯฮท ฯฯฮฝ ฮตฮฝฮฝฮฟฮนฯฮฝ ฮบฮฑฮน ฯฯฮฝ ฮฝฯฮผฯฮฝ ฯฮฟฯ ฯฮฟฮผฮญฮฑ ยซฮฮนฮฝฮทฮผฮฑฯฮนฮบฮฎยป
(ฮฮปฮญฯฮต ฯฮทฮฝ ฮฑฮฝฮฌฯฯฮทฯฮท ฯฯฮฟ blog ฮผฮฟฯ ยซฮฮน ฮณฯฮฑฯฮนฮบฮญฯ ฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯ, ฮฟฮน ฮดฯ ฯฮบฮฟฮปฮฏฮตฯ ฯฯฮฝ ฮผฮฑฮธฮทฯฯฮฝ ฮบฮฑฮน ฮท ฯฮฑฮนฮดฮฑฮณฯฮณฮนฮบฮฎ ฮนฮดฮญฮฑ ฯฯฮฝ ฮผฮตฯฮฑฮฒฮฌฯฮตฯฮฝ ฮฑฯฯ ฮผฮนฮฑ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท ฯฮต ฮฌฮปฮปฮตฯยป (http://makolas.blogspot.com/2011/10/blog-post_15.htmlย ).
ฮฯฮนฯฮปฮญฮฟฮฝ, ฯฯฮนฯ ฯฯฮฟฯฮฌฯฮตฮนฯ ฮผฮฟฯ ฯ ฯฮฟฯฯฮทฯฮฏฮถฯ ฯฯฮน ฮธฮฑ ฯฯฮญฯฮตฮน ฮฝฮฑ ฮดฮนฮฑฮผฮฟฯฯฯฯฮฟฯ ฮผฮต ฯฮฟฯ ฯ ฮตฮนฮดฮนฮบฮฟฯฯ ฯฯฯฯฮฟฯ ฯ ฮดฮนฮดฮฑฯฮบฮฑฮปฮฏฮฑฯ ฮบฮฑฮน ฮผฮฌฮธฮทฯฮทฯ ฮญฯฯฮน ฯฯฯฮต ฮฝฮฑ ฮปฮฑฮผฮฒฮฌฮฝฮฟฮฝฯฮฑฮน ฯฮทฯฮฌ ฯ ฯฯฯฮท ฯฮฑ ฮผฮญฯฮฑ (ฮฎ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝฯฮฑ) ฮตฮฝฮฑฯฯฯฮปฮทฯฮทฯ ฯฯฮฝ ฮผฮฑฮธฮทฯฯฮฝ ฮบฮฑฮธฯฯ ฮบฮฑฮน ฮฟฮน ฮตฮผฯฮปฮตฮบฯฮผฮตฮฝฮตฯ ฮบฮฌฮธฮต ฯฮฟฯฮฌ ฮฑฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯ. ฮฮต ฮฌฮปฮปฮฑ ฮปฯฮณฮนฮฑ ฮฟฮน ฯฯฮฟฯฮตฮนฮฝฯฮผฮตฮฝฮตฯ ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฯฮตฯฮนฮปฮฑฮผฮฒฮฌฮฝฮฟฯ ฮฝ ฯฯ ฮฝฮดฯ ฮฑฯฯฮนฮบฮฌ ฯฯฯฮฟ ฯฮฑ applets ฯฯฮฟ ฮบฮฑฮน ฯฮฑ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝฯฮฑ {ยซฯฮฑฯฯฮฏ โ ฮผฮฟฮปฯฮฒฮนยป ฮบฮฑฮน ยซฮดฮนฮฑฮดฯฮฑฯฯฮนฮบฯฯ ฯฮฏฮฝฮฑฮบฮฑฯยป} ฮผฮต ฯฯ ฮณฮบฮตฮบฯฮนฮผฮญฮฝฮฟฯ ฯ ฯฯฯฯฮฟฯ ฯ ฯฮฟฯ ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฮดฮนฮฑฯฯ ฯฯฮฝฮฟฮฝฯฮฑฮน, ฮณฮนฮฑ ฯฮฑฯฮฌฮดฮตฮนฮณฮผฮฑ, ฯฯ ฮตฮพฮฎฯ:
ฮฮฟฮฝฯฮฟฮปฮฟฮณฮฏฯ ฮดฮฏฮฝฮตฯฮฑฮน ฮท ฮตฯ ฮบฮฑฮนฯฮฏฮฑ ฯฯฮฟฯ ฯ ฮผฮฑฮธฮทฯฮญฯ ฮฝฮฑ ฮตฮฏฮฝฮฑฮน ฮตฮฝฮตฯฮณฮฟฮฏ ฮบฮฌฮฝฮฟฮฝฯฮฑฯ ฯฯฮฌฮณฮผฮฑฯฮฑ ฮบฮฑฮน ฮฝฮฑ ฯฯ ฮปฮปฮฟฮณฮฏฮถฮฟฮฝฯฮฑฮน ฯฮตฮนฯฮฑฮผฮฑฯฮนฮถฯฮผฮตฮฝฮฟฮน ฯฮต ฯฯ ฮณฮบฮตฮบฯฮนฮผฮญฮฝฮฟ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ. ฮฮน ฯฯฮฟฯฮตฮนฮฝฯฮผฮตฮฝฮตฯ ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮดฮฏฮฝฮฟฯ ฮฝ ฮญฮผฯฮฑฯฮท ฯฯฮฑ ฯฮฟฮนฮฟฯฮนฮบฮฌ ฯฮฑฯฮฑฮบฯฮทฯฮนฯฯฮนฮบฮฌ ฯฮตฯฮนฯฯฯฯฮตฯฮฟ ฮฑฯฯ ฯฯฮน ฯฯฮฑ ฯฮฟฯฮฟฯฮนฮบฮฌ-ฯ ฯฮฟฮปฮฟฮณฮนฯฯฮนฮบฮฌ. ฮฮนฮฑ ฯฮฑฯฮฌฮดฮตฮนฮณฮผฮฑ, ฮฟฮน ฮผฮฑฮธฮทฯฮญฯ ฮฑฮฝฮฑฯฯฯฮนฮฟฯฮฝฯฮฑฮน ฯฯฮน ฮผฯฮฝฮฟ ฮณฮนฮฑ ฯฮฟ ยซฯฮน ฮตฮฏฮฝฮฑฮนยป ฮตฯ ฮธฯฮณฯฮฑฮผฮผฮท ฮฟฮผฮฑฮปฮฌ ฮตฯฮนฯฮฑฯฯ ฮฝฯฮผฮตฮฝฮท ฮบฮฏฮฝฮทฯฮท ฮฑฮปฮปฮฌ ฮบฮฑฮน ฮณฮนฮฑ ฯฮฟ ยซฯฮน ฮดฮตฮฝ ฮตฮฏฮฝฮฑฮนยป ฯฯฯฯ ฯฯฮฝฮนฮถฮต ฮผฮต ฮญฮผฯฮฑฯฮท ฮฟ ฮฮฝฯฯฮญฮฑฯ ฮ. ฮฮฑฯฯฮญฯฮฑฯ.
ฮฃฯฮผฯฯฮฝฮฑ ฮผฮต ฯฮฑ ฯฮฑฯฮฑฯฮฌฮฝฯ ฮฟฮน ฮผฮฑฮธฮทฯฮญฯ ฯฮฌฮฝฯฮฑ ฮญฯฮฟฯ ฮฝ ฯฯฮท ฮดฮนฮฌฮธฮตฯฮฎ ฯฮฟฯ ฯ ฮผฮนฮฑ ยซฯฯฮฟฮฒฮปฮทฮผฮฑฯฮนฮบฮฎ ฮบฮฑฯฮฌฯฯฮฑฯฮทยป (ฮญฮฝฮฑ ฯฯฮฝฮฟฮปฮฟ ฯฮปฮทฯฮฟฯฮฟฯฮนฯฮฝ ฮบฮฑฮน ฮบฮฑฮธฮทฮบฯฮฝฯฯฮฝ ฮผฮต ฮผฮฟฯฯฮฎ ฯฮฟฮนฮบฮนฮปฯฮฝ ฮฑฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฯฮฝ ฯฯฯฯ ฮฮตฮบฯฮนฮบฮฎ, ฮฮปฮณฮตฮฒฯฮนฮบฮฎ, ฮ ฮฏฮฝฮฑฮบฮฑฯ ฯฮนฮผฯฮฝ, ฮฯฮฌฯฮทฮผฮฑ ) ฮบฮฑฮน ฯฯฮท ฯฯ ฮฝฮญฯฮตฮนฮฑ ฯฯฮฟฯฯฯฮฟฯฮฝ ฯฯฮนฯ ฮฑฯฮฑฮฝฯฮฎฯฮตฮนฯ ฯฮฟฯ ฯ ฮฑฮบฮฟฮปฮฟฯ ฮธฯฮฝฯฮฑฯ grosso modo ฯฮทฮฝ ฯฮฑฯฮฑฮดฮฟฯฮนฮฑฮบฮฎ ยซฯฮตฮนฯฮฑฮผฮฑฯฮนฮบฮฎ ฮผฮญฮธฮฟฮดฮฟ ฮญฯฮตฯ ฮฝฮฑฯยป
(ฮฒฮปฮญฯฮต ฮญฮฝฮฑ ฯฮฑฮปฮนฯ ฮฌฯฮธฯฮฟ ฮผฮฟฯ ยซH ฮญฮฝฯฮฑฮพฮท ฯฮทฯ ยซฮ ฮตฮนฯฮฑฮผฮฑฯฮนฮบฮฎฯ ฮฮตฮธฯฮดฮฟฯ ฮฯฮตฯ ฮฝฮฑฯยป ฯฯฮฟ ฮฃฯฮฟฮปฮตฮฏฮฟยปย http://makolas.blogspot.gr/2013/07/h.html ) ฯฯฯฯ ฮญฯฮตฮน ฮบฮฑฮธฮนฮตฯฯฮธฮตฮฏ ฮณฮนฮฑ ฯฮนฯ ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮผฮต ฯฮตฮนฯฮฌฮผฮฑฯฮฑ ฯฯฮฟ ฯฯฮฟฮปฮนฮบฯ ฮตฯฮณฮฑฯฯฮฎฯฮนฮฟ.
ฮคฮตฮปฮนฮบฮฌ, ฮญฯฯฮนฮฑฮพฮฑย ฮญฮฝฮฑ ฮผฮนฮบฯฯ appletย ฯฯฮฟ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ ฯฮฟฯ Scratch ฮบฮฑฮน ฯฮฑ ฮฑฮฝฮฌฯฯฮทฯฮฑ ฯฯฮฟ Scratch Website: ฮฮพฮนฮฟฯฮฟฮนฮตฮฏ ฯฮฟ project ฯฮฟฯ ฯฮตฯฮนฮปฮฑฮผฮฒฮฌฮฝฮตฮน ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t), ฯฮฟฮฝ ฯฮฏฮฝฮฑฮบฮฑ ฯฮฑฯฯ ฯฮฎฯฯฮฝ ฮบฮฑฮน ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฮตฮฝฯฯ ฯฮฑฮนฮดฮนฮฟฯ.
ฮ. ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮผฮต ฯฮฟ applet Scratch ยซฮฯฯ ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t) ฯฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฮบฮฏฮฝฮทฯฮทฯยป (http://scratch.mit.edu/projects/dapontesgr/2202942 )
ฮคฮฟ ฯฮฑฯฮฑฯฮฌฮฝฯ applet Scratch ฮตฯฮนฯฯฮญฯฮตฮน ฯฮท ฮดฮนฮฑฮผฯฯฯฯฯฮท ฯฮฟฯ ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ (x,t) ฮผฮต ฯฮท ฮฒฮฟฮฎฮธฮตฮนฮฑ ฯฮฟฯ ฮดฮตฮฏฮบฯฮท ฯฮฟฯ ฯฮฟฮฝฯฮนฮบฮนฮฟฯ: ฮบฮฌฮฝฮฟฮฝฯฮฑฯ ฮบฮปฮนฮบ ฮบฮฑฮน ฯฯฯฯฮนฮผฮฟ ฯฯฮฝ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฯฮฝยป – ฯฮฟฯ ฮตฮฝฯฮฝฮฟฮฝฯฮฑฮน ฮผฮตฯฮฑฮพฯ ฯฮฟฯ ฯ ฮผฮต ฮผฮนฮฑ ฮณฯฮฑฮผฮผฮฎ – ฯฯ ฮฝฮนฯฯฮฟฯฮฝ ฯฮตฮปฮนฮบฮฌ ฮญฮฝฮฑ ฮณฯฮฌฯฮทฮผฮฑ (x,t) ฯฯฮฟ ฮฮฑฯฯฮตฯฮนฮฑฮฝฯ ฮฃฯฯฯฮทฮผฮฑ ฮฃฯ ฮฝฯฮตฯฮฑฮณฮผฮญฮฝฯฮฝ. ฮฃฯฮท ฯฯ ฮฝฮญฯฮตฮนฮฑ, ฮผฮต ฮบฮปฮนฮบ ฯฯฮฟ ฮบฮฟฯ ฮผฯฮฏ ยซฮพฮตฮบฮฏฮฝฮฑยป ฯฮฑฯฮฑฮบฮฟฮปฮฟฯ ฮธฮฟฯฮผฮต ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฯฮผฯฯฮฝฮฑ ฮผฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t). ฮฮฝฮดฮนฮฑฯฮญฯฮฟฮฝ ฯฮฑฯฮฟฯ ฯฮนฮฌฮถฮตฮน ฮท ฮดฯ ฮฝฮฑฯฯฯฮทฯฮฑ ฯฮฟฯ ฯฯฮฟฯฯฮญฯฮตฮน ฯฮฟ ฯฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ: ฮผฯฮปฮนฯ ฮฟ ฮดฮตฮฏฮบฯฮทฯ ฯฮฟฯ ฯฮฟฮฝฯฮนฮบฮนฮฟฯ ฮฑฮณฮณฮฏฮพฮตฮน ฮญฮฝฮฑ ฮฑฯฯ ฯฮฑ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฮฑยป ฯฮฟฯ ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฮผฮฑฯ ฮญฮฝฮฑ ฮผฮฎฮฝฯ ฮผฮฑ ฮผฮฑฯ ฯฮปฮทฯฮฟฯฮฟฯฮตฮฏ ฮณฮนฮฑ ฯฮนฯ ฮฑฮปฮณฮตฮฒฯฮนฮบฮญฯ ฯฮนฮผฮญฯ ฯฮทฯ ฮธฮญฯฮทฯ ฯฮฟฯ ฮบฮนฮฝฮทฯฮฟฯ ฮบฮฑฮธฯฯ ฮบฮฑฮน ฯฮทฮฝ ฮฑฮฝฯฮฏฯฯฮฟฮนฯฮท ฯฯฮฟฮฝฮนฮบฮฎ ฯฯฮนฮณฮผฮฎ.
ฮโ ฮฑฯ ฯฯฮฝ ฯฮฟฮฝ ฯฯฯฯฮฟ ฮตฯฮนฯฯ ฮณฯฮฌฮฝฮตฯฮฑฮน ฮท ยซฮฑฮฝฮฌฮบฯฮนฯฮทยป ฯฯฮฝ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฯฮฝยป ฯฮฟฯ ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฮบฮฑฮน ฮท ฯฯ ฮฝฮฑฮณฯฮณฮฎ ฯฯ ฮผฯฮตฯฮฑฯฮผฮฌฯฯฮฝ.ย
ฮฯฮนฯฮปฮญฮฟฮฝ, ฮฟฮน ฮฑฮปฮณฮตฮฒฯฮนฮบฮญฯ ฯฮนฮผฮญฯ ฯฮทฯ ฯฮฑฯฯฯฮทฯฮฑฯ ฯฮฟฯ ฮบฮนฮฝฮทฯฮฟฯ ฮตฮผฯฮฑฮฝฮฏฮถฮฟฮฝฯฮฑฮน ฯฮต ฮผฮฟฮฝฮฟฮดฮนฮฌฯฯฮฑฯฮฟ ฯฮฏฮฝฮฑฮบฮฑ. ฮ ฯฯฮบฮตฮนฯฮฑฮน ฮณฮนฮฑ ฯฮนฮผฮญฯ ฯฮฟฯ ฮฑฮฝฯฮนฯฯฮฟฮนฯฮฟฯฮฝ ฯฮต ฮบฮฑฮธฮญฮฝฮฑ ฮฑฯฯ ฯฮฑ ฮตฯฯฮฌ ฮตฯ ฮธฯฮณฯฮฑฮผฮผฮฑ ฯฮผฮฎฮผฮฑฯฮฑ ฯฮฟฯ ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฯฯฯฮต ฮฝฮฑ ฮตฮปฮญฮณฯฮตฯฮฑฮน ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฮบฮฑฯฮฌ ฯฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฯฮทฯ ฮดฮนฮฑฮผฯฯฯฯฯฮฎฯ ฯฮฟฯ .
ฮฯฮฟฮฝ ฮฑฯฮฟฯฮฌ ฯฮทฮฝ ฯฮฑฯฮฑฮบฮฟฮปฮฟฯฮธฮทฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฮฟฯ ฯฮฑฮนฮดฮนฮฟฯ ฯฯฮฟฮฝ ฮฌฮพฮฟฮฝฮฑ โ x, ฮผฮตฯฮฌ ฮฑฯฯ ฯฯฯฮปฮนฮฟ-ฯ ฯฯฮดฮตฮนฮพฮท ฮตฮฝฯฯ ฮผฮฑฮธฮทฯฮฎ ฯฯฮฟ Scratch website, ฯฯฯฯฮธฮตฯฮฑ ฮผฮนฮฑ ฮบฮฑฯฮฑฮบฯฯฯ ฯฮท ฯฯฮฌฯฮนฮฝฮท ฮณฯฮฑฮผฮผฮฎ ฯฮฟฯ ฮผฮตฯฮฑฮบฮนฮฝฮตฮฏฯฮฑฮน ฯฯ ฮฝฮตฯฯฯ ฮดฮตฮฏฯฮฝฮฟฮฝฯฮฑฯ ฯฮฟ ฮฑฮฝฯฮฏฯฯฮฟฮนฯฮฟ ฯฮทฮผฮตฮฏฮฟ ฯฮฟฯ ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ. ฮ ฯฯฮบฮตฮนฯฮฑฮน ฮณฮนฮฑ ฮญฮฝฮฑ ฮตฮฝฮดฮนฮฑฯฮญฯฮฟฮฝ ฮฒฮฟฮทฮธฮทฯฮนฮบฯ ฮตฯฮณฮฑฮปฮตฮฏฮฟ ฮตฮปฮญฮณฯฮฟฯ ฮผฮตฯฮฑฮพฯ ฮดฯฮฟ ฮฑฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฯฮฝ.
(A) ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฯฯ ฯฮท ฮปฮตฮบฯฮนฮบฮฎ ฯฮตฯฮนฮณฯฮฑฯฮฎ ฮบฮฏฮฝฮทฯฮทฯ ฮผฮนฮฑฯ ฮผฯฮฝฮฟ ฯฮฌฯฮทฯ ฯฯฮทฮฝ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮฏฮทฯฮท ฯฮทฯ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮฎ ฯฮทฯย
ฮฮฑฮธฯฯ ฮญฯฯฮนฮฑฯฮฝฮฑ ฯฮฟ project ฯฮบฮตฯฯฯฮผฮฟฯ ฮฝฮฑ ฯฯฮน ฮฑฯ ฯฯ ฮธฮฑ ฮตฮฏฮฝฮฑฮน ฯฯฮฎฯฮนฮผฮฟ ฮผฯฮฝฮฟ ฮณฮนฮฑ ฯฮทฮฝ ฮฑฯฮปฮฟฯฯฯฮตฯฮท ฯฯฮฝ ฮบฮนฮฝฮฎฯฮตฯฮฝ ฯฮฟฯ ฮดฮนฮดฮฌฯฮบฮฟฯ ฮผฮต ฯฯฮฟ ฯฯฮฟฮปฮตฮฏฮฟ ฮดฮทฮปฮฑฮดฮฎ ฯฮทฮฝ ยซฮฯ ฮธฯฮณฯฮฑฮผฮผฮท ฮฮผฮฑฮปฮฎ ฮฮฏฮฝฮทฯฮทยป. ฮฃฯฮท ฯฯ ฮฝฮญฯฮตฮนฮฑ ฮตฮฏฮดฮฑ ฯฯฮน ฮผฯฮฟฯฯ ฮฝฮฑ ฯฮฑฮฝฯฮฌฮถฮฟฮผฮฑฮน ฮบฮฑฮน ฮฝฮฑ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฯ ฮบฮฑฮน ฮฌฮปฮปฮตฯ ฮณฮฝฯฯฯฮญฯ ฮบฮนฮฝฮฎฯฮตฮนฯ ฮฑฮปฮปฮฌ ฮฑฯ ฯฯ ฮผฯฮฝฮฟ ฮผฮต ฮผฮตฮณฮฌฮปฮท ฯฯฮฟฯฮญฮณฮณฮนฯฮท! ฮฯฯ ฯฮฟฮฝ ฯฯฯฯฮฟ ฯฮฟฯ ฯฯฮฟฮณฯฮฑฮผฮผฮฑฯฮฏฯฯฮทฮบฮต ฯฮฟ applet ฮดฮตฮฝ ฮพฮตฯฮฝฮฌฯ ฯฯฮน ฯฮต ฮบฮฑฮธฮตฮผฮนฮฌ ฮฑฯฯ ฯฮนฯ ฮตฯฮนฮผฮญฯฮฟฯ ฯ ฮตฯฯฮฌ ย ฯฮฌฯฮตฮนฯ ฮท ฯฮฑฯฯฯฮทฯฮฑ ฯฮฑฯฮฑฮผฮญฮฝฮท ฯฯฮฑฮธฮตฯฮฎ. ฮฯฮฝฮฟ ฮฑฮฝ ฮญฯฯฮนฮฑฯฮฝฮฑ ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t) ฯฯฮทฯฮนฮผฮฟฯฮฟฮนฯฮฝฯฮฑฯ ฮญฮฝฮฑ ฯฮฟฮปฯ ฮผฮตฮณฮฌฮปฮฟ ฯฮปฮฎฮธฮฟฯ ยซฯฮทฮผฮตฮฏฯฮฝยป ฮธฮฑ ฮบฮฑฯฮฌฯฮตฯฮฝฮฑ ฮฝฮฑ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮฎฯฯ ฯฮนฮฟ ฮนฮบฮฑฮฝฮฟฯฮฟฮนฮทฯฮนฮบฮฌ ฯฮนฯ ฮบฮนฮฝฮฎฯฮตฮนฯ.
A.1.ย [ฮฮตฮบฯฮนฮบฮฎ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท]ย ฮฆฮฑฮฝฯฮฑฮถฯฮผฮฑฯฯฮต ฯฮฟ ฯฮฑฮนฮดฮฏ ฮฝฮฑ ฮบฮนฮฝฮตฮฏฯฮฑฮน ฮตฯ ฮธฯฮณฯฮฑฮผฮผฮฑ ฯฯฮฟ ฮดฯฯฮผฮฟ (ฮฌฮพฮฟฮฝฮฑฯโx) ฯฯฮฟฯ ฯฮฑ ฮดฮตฮพฮนฮฌ ฮผฮต ฯฯฮฑฮธฮตฯฮฎ ฯฮฑฯฯฯฮทฯฮฑ ฯ =1 ฮผฮฟฮฝฮฌฮดฮฑ. ฮคฮท ฯฯฮฟฮฝฮนฮบฮฎ ฯฯฮนฮณฮผฮฎ t=0 ฯฮฟ ฯฮฑฮนฮดฮฏ ฯฮตฯฮฝฮฌฮตฮน ฮฑฯฯ ฯฮท ฮธฮญฯฮท x0=-83 pixels ฮบฮฑ ฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฮบฮฏฮฝฮทฯฮทฯ ฮตฮฏฮฝฮฑฮน 230 ฮผฮฟฮฝฮฌฮดฮตฯ ฯฯฯฮฝฮฟฯ .
i) ฮฮต ฮบฮปฮนฮบ ฮบฮฑฮน ฯฯฯฯฮนฮผฮฟ ฯฯฮฑ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฮฑยป ฮดฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฯฮทฮฝ ฮฟฮธฯฮฝฮท ฯฮฟฯ ฯ ฯฮฟฮปฮฟฮณฮนฯฯฮฎ ฮญฯฯฮน ฯฯฯฮต ฮฝฮฑ ฯฮฑฯฮฑฮบฮฟฮปฮฟฯ ฮธฮฎฯฮตฯฮต ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฮฟฯ ฯฮฑฮนฮดฮนฮฟฯ.
ii) ฮฮฑฯฮนฮถฯฮผฮตฮฝฮฟฮน ฯฯฮนฯ ฯฮนฮผฮญฯ ฯฮฟฯ ฮผฯฮฟฯฮตฮฏฯฮต ฮฝฮฑ ฮฑฮฝฯฮปฮฎฯฮตฯฮต ฮฑฯฯ ฯฮฑ ยซฯฮทฮผฮตฮฏฮฑยป ฯฮฟฯ ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ — ฮฝฮฑ ฯ ฯฮฟฮปฮฟฮณฮฏฯฮตฯฮต ฯฮท ฮผฮตฯฮฑฯฯฯฮนฯฮท ฯฮฟฯ ฯฮฑฮนฮดฮนฮฟฯ ฮบฮฑฯฮฌ ฯฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฯฯฮฝ 230 ฮผฮฟฮฝฮฌฮดฯฮฝ ฯฯฯฮฝฮฟฯ . —ฮฝฮฑ ฮฑฯฮฟฮดฮตฮฏฮพฮตฯฮต ฯฯฮน ฮท ฮบฮปฮฏฯฮท ฯฮฟฯ ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฯฯ ฯฯฮฟฯ ฯฮฟฮฝ ฮฌฮพฮฟฮฝฮฑ โt ฮตฮฏฮฝฮฑฮน 45 ฮผฮฟฮฏฯฮตฯ.
iii) ฮฮฑ ฮฒฯฮตฮฏฯฮต ฯฮทฮฝ ฮตฮพฮฏฯฯฯฮท ฮบฮฏฮฝฮทฯฮทฯ ฮณฮนฮฑ ฯฮท ฮธฮญฯฮท ฯฮฟฯ ฮบฮนฮฝฮทฯฮฟฯ
ฮ.2. [ฮฮตฮบฯฮนฮบฮฎ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท]ย ฮฆฮฑฮฝฯฮฑฮถฯฮผฮฑฯฯฮต ฯฮฟ ฯฮฑฮนฮดฮฏ ฮฝฮฑ ฮบฮนฮฝฮตฮฏฯฮฑฮน ฮตฯ ฮธฯฮณฯฮฑฮผฮผฮฑ ฮผฮต ฯฮฑฯฯฯฮทฯฮฑ ฯ =-0.5 ฮผฮฟฮฝฮฌฮดฮตฯ. ฮคฮท ฯฯฮนฮณฮผฮฎ t=0 ฯฮฟ ฯฮฑฮนฮดฮฏ ฮดฮนฮญฯฯฮตฯฮฑฮน ฮฑฯฯ ฯฮทฮฝ ฮฑฯฯฮฎ ฯฮฟฯ ฮฌฮพฮฟฮฝฮฑ โx ฮบฮฑฮน ฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฮบฮฏฮฝฮทฯฮทฯ ฮตฮฏฮฝฮฑฮน 230 ฮผฮฟฮฝฮฌฮดฮตฯ ฯฯฯฮฝฮฟฯ .
i) ฮฮต ฮบฮปฮนฮบ ฮบฮฑฮน ฯฯฯฯฮนฮผฮฟ ฯฯฮฑ ฮฟฮบฯฯ ยซฯฮทฮผฮตฮฏฮฑยป ฮดฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฯฮทฮฝ ฮฟฮธฯฮฝฮท ฯฮฟฯ ฯ ฯฮฟฮปฮฟฮณฮนฯฯฮฎ ฮญฯฯฮน ฯฯฯฮต ฮฝฮฑ ฯฮฑฯฮฑฮบฮฟฮปฮฟฯ ฮธฮฎฯฮตฯฮต ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ ฯฮฟฯ ฯฮฑฮนฮดฮนฮฟฯ.
ii) ฮฮฑฯฮนฮถฯฮผฮตฮฝฮฟฮน ฯฯฮนฯ ฯฮนฮผฮญฯ ฯฮฟฯ ฮผฯฮฟฯฮตฮฏฯฮต ฮฝฮฑ ฮฑฮฝฯฮปฮฎฯฮตฯฮต ฮฑฯฯ ฯฮฑ ยซฯฮทฮผฮตฮฏฮฑยป ฯฮฟฯ ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ
— ฮฝฮฑ ฯ ฯฮฟฮปฮฟฮณฮฏฯฮตฯฮต ฯฮท ฮผฮตฯฮฑฯฯฯฮนฯฮท ฯฮฟฯ ฯฮฑฮนฮดฮนฮฟฯ ฮบฮฑฯฮฌ ฯฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฯฯฮฝ 230 ฮผฮฟฮฝฮฌฮดฯฮฝ ฯฯฯฮฝฮฟฯ
—ฮฝฮฑ ฯ ฯฮฟฮปฮฟฮณฮฏฯฮตฯฮต ฯฮทฮฝ ฮบฮปฮฏฯฮท ฯฮฟฯ ฮณฯฮฑฯฮฎฮผฮฑฯฮฟฯ ฯฯ ฯฯฮฟฯ ฯฮฟฮฝ ฮฌฮพฮฟฮฝฮฑ โt.
iii) ฮฮฑ ฮฒฯฮตฮฏฯฮต ฯฮทฮฝ ฮตฮพฮฏฯฯฯฮท ฮบฮฏฮฝฮทฯฮทฯ ฮณฮนฮฑ ฯฮท ฮธฮญฯฮท ฯฮฟฯ ฮบฮนฮฝฮทฯฮฟฯ
B.1. ฮ ฮตฮพฮฏฯฯฯฮท ฮบฮฏฮฝฮทฯฮทฯ ฮณฮนฮฑ ฯฮท ฮธฮญฯฮท ฯฮฟฯ ฯฮฑฮนฮดฮนฮฟฯ [ฮฑฮปฮณฮตฮฒฯฮนฮบฮฎ ฮฑฮฝฮฑฯฮฑฯฮฌฯฯฮฑฯฮท] ฮตฮฏฮฝฮฑฮนย x(t) = 100 – t ฮบฮฑฮน ฮท ฮดฮนฮฌฯฮบฮตฮนฮฑ ฯฮทฯ ฮตฮฏฮฝฮฑฮน 200 ฮผฮฟฮฝฮฌฮดฮตฯ ฯฯฯฮฝฮฟฯ .
i) ฮ ฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮฎฯฯฮต ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ
ii) ฮงฯฮทฯฮนฮผฮฟฯฮฟฮนฯฮฝฯฮฑฯ ฯฮทฮฝ ฮตฮพฮฏฯฯฯฮท ฮบฮฏฮฝฮทฯฮทฯ ฯ ฯฮฟฮปฮฟฮณฮฏฯฯฮต ฯฮท ฮธฮญฯฮท ฯฮฟฯ ฯฮฑฮนฮดฮนฮฟฯ ฯฮท ฯฯฮฟฮฝฮนฮบฮฎ ฯฯฮนฮณฮผฮฎ t=200 ฮผฮฟฮฝฮฌฮดฮตฯ ฯฯฯฮฝฮฟฯ .
iii) ฮฯฮนฮฒฮตฮฒฮฑฮนฯฯฯฮต ฯฮทฮฝ ฮฟฯฮธฯฯฮทฯฮฑ ฯฮทฯ ฮฑฯฮฌฮฝฯฮทฯฮทฯ ฮฑฯฯ ฯฮนฯ ฯฮปฮทฯฮฟฯฮฟฯฮฏฮตฯ ฯฮฟฯ ฯฮฑฯ ฯฮฑฯฮญฯฮตฮน ฯฮฟ applet.
(ฮ) ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฮท ฮฟฮผฮฑฮปฮฌ ฮผฮตฯฮฑฮฒฮฑฮปฮปฯฮผฮตฮฝฮตฯ ฮบฮนฮฝฮฎฯฮตฮนฯ
ฮฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฯฯฮต ฮท ฮบฮฏฮฝฮทฯฮท ฯฮฟฯ ฯฮฑฮนฮดฮนฮฟฯ ฯฯฮฟฮฝ ฮฌฮพฮฟฮฝฮฑ x:
ฮ.1.ฮฮฑ ฮตฮฏฮฝฮฑฮน ฮฑฯ ฮพฮฑฮฝฯฮผฮตฮฝฮทฯ ฯฮฑฯฯฯฮทฯฮฑฯ ฮบฮฑฯฮฌ ฯฯฮฟฮฝฮนฮบฮฌ ฮดฮนฮฑฯฯฮฎฮผฮฑฯฮฑ
ฮ.2. ฮฮฑ ฮตฮฏฮฝฮฑฮน ฮตฮปฮฑฯฯฮฟฯฮผฮตฮฝฮทฯ ฯฮฑฯฯฯฮทฯฮฑฯ
ฮ.3. ฮฮฑ ฮตฮฏฮฝฮฑฮน ฮฑฯ ฮพฮฑฮฝฯฮผฮตฮฝฮท ฮผฮญฯฯฮน ฯฮทฮฝ ฮฑฯฯฮฎ ฯฮฟฯ ฮฌฮพฮฟฮฝฮฑ ฮบฮฑฮน ฯฯฮท ฯฯ ฮฝฮญฯฮตฮนฮฑ ฮตฮปฮฑฯฯฮฟฯฮผฮตฮฝฮท.
ฮ.4. ฮฮฑ ยซฮผฮฟฮนฮฌฮถฮตฮนยป ฮผฮต ฮฑฯ ฯฮฎฮฝ ฯฮทฯ ฯฮฑฮปฮฌฮฝฯฯฯฮทฯ ฮผฮนฮฑฯ ฯฮตฯฮนฯฮดฮฟฯ .
ฮ. ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฯฮฌฯฮทฮผฮฑ (x,t) ฮผฮต ฮดฮนฮฑฮบฯฮนฯฮญฯ ฯฮฌฯฮตฮนฯ (ฮผฮต ฯ =ฯฯฮฑฮธฮตฯฯ, ฯ =0)
ฮ.1.ย ฮคฮท ฯฯฮฟฮฝฮนฮบฮฎ ฯฯฮนฮณฮผฮฎ t=0 ฯฮฟ ฯฮฑฮนฮดฮฏ ฯฮตฯฮฝฮฌฮตฮน ฮฑฯฯ ฯฮทฮฝ ฮฑฯฯฮฎ ฯฮฟฯ ฯฯฮฟฯฮฑฮฝฮฑฯฮฟฮปฮนฯฮผฮญฮฝฮฟฯ ฮฌฮพฮฟฮฝฮฑ ฮบฮฑฮน ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮตฮฏ ฮตฯ ฮธฯฮณฯฮฑฮผฮผฮท ฮฟฮผฮฑฮปฮฎ ฮบฮฏฮฝฮทฯฮท ฯฯฮฟฯ ฯฮฑ ฮดฮตฮพฮนฮฌ ฮบฮฑฮน ฯฯฮท ฯฯ ฮฝฮญฯฮตฮนฮฑ ฯฮฑฯฮฑฮผฮญฮฝฮตฮน ฮฑฮบฮฏฮฝฮทฯฮฟ ฮณฮนฮฑ ฯฯฯฮฝฮฟ 30 ฮผฮฟฮฝฮฌฮดฯฮฝ. ฮฮตฯฮฌ ฯฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮตฮฏ ฮบฮฏฮฝฮทฯฮท ฮผฮต ฯฯฮฑฮธฮตฯฮฎ ฯฮฑฯฯฯฮทฯฮฑ ฮบฮฑฮน ฯฮตฮปฮตฮนฯฮฝฮตฮน ฮผฯฮปฮนฯ ฯฮฟ ฯฮฑฮนฮดฮฏ ฮตฯฮนฯฯฯฮญฯฮตฮน ฯฯฮทฮฝ ฯฯฮทฮฝ ฮฑฯฯฮฎ ฯฮฟฯ ฮฌฮพฮฟฮฝฮฑ x.ย
i) ฮฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฮฟฯ ฮฑฮฝฯฮนฯฯฮฟฮนฯฮตฮฏ ฯฯฮท ฮปฮตฮบฯฮนฮบฮฎ ฯฮตฯฮนฮณฯฮฑฯฮฎ.
ii) ยซฮคฯฮญฮพฯฮตยป ฯฮทฮฝ ฯฯฮฟฯฮฟฮผฮฟฮฏฯฯฮท ฮผฮต ฯฮบฮฟฯฯ ฮฝฮฑ ฮฒฮตฮฒฮฑฮนฯฮธฮตฮฏฯฮต ฮณฮนฮฑ ฯฮทฮฝ ฮฟฯฮธฯฯฮทฯฮฑ ฯฮทฯ ฮปฮตฮบฯฮนฮบฮฎฯ ฯฮตฯฮนฮณฯฮฑฯฮฎฯ.
ฮ. ฮฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฯฮทฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮฑฯ:ย ฮฯฯ ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ (x,t) ฯฯฮท ฮปฮตฮบฯฮนฮบฮฎ ฯฮตฯฮนฮณฯฮฑฯฮฎ ฯฮทฯ ฮบฮฏฮฝฮทฯฮทฯ
ฮ.1. ฮฮฏฮฝฮตฯฮฑฮน ฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ:
ii) ฮ ฯฮฑฮณฮผฮฑฯฮฟฯฮฟฮนฮฎฯฯฮต ฯฮนฯ ฯฯฮฟฯฮฟฮผฮฟฮนฯฯฮตฮนฯ ฮผฮต ฮฒฮฌฯฮท ฯฮฑ ฮณฯฮฑฯฮฎฮผฮฑฯฮฑ ฮบฮฑฮน ฮตฯฮนฮฒฮตฮฒฮฑฮนฯฯฯฮต ฯฮทฮฝ ฮฟฯฮธฯฯฮทฯฮฑ ฯฯฮฝ ฮปฮตฮบฯฮนฮบฯฮฝ ฯฮตฯฮนฮณฯฮฑฯฯฮฝ.
iii) ฮฅฯฮฟฮปฮฟฮณฮฏฯฯฮต ฯฮฑฯฯฯฮทฯฮตฯ, ฮผฮตฯฮฑฯฮฟฯฮฏฯฮตฮนฯ ฮบฮฑฮน ฯฯฮฟฮฝฮนฮบฮญฯ ฮดฮนฮฌฯฮบฮตฮนฮตฯ ฮผฮต ฮฒฮฌฯฮท ฯฮนฯ ฯฮปฮทฯฮฟฯฮฟฯฮฏฮตฯ ฯฮฟฯ ฮดฮฏฮฝฮฟฮฝฯฮฑฮน ฯฯฮฟ ฮณฯฮฌฯฮทฮผฮฑ.
ฮ. ฮฮฏฮฝฮฟฮฝฯฮฑฮน ฮดฯฮฟ ฮณฯฮฑฯฮนฮบฮญฯ ฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯ (ฮธฮญฯฮทฯ, ฯฯฯฮฝฮฟฯ ) ฯฯฮฟ ฮฏฮดฮนฮฟ ฮณฯฮฌฯฮทฮผฮฑ ฯฮฟฯ ฮฑฮฝฮฑฯฮญฯฮฟฮฝฯฮฑฮน ฯฯฮทฮฝ ฮบฮฏฮฝฮทฯฮท ฮตฮฝฯฯ ฮบฮฟฯฮนฯฯฮนฮฟฯ ฮบฮฑฮน ฮตฮฝฯฯ ฮฑฮณฮฟฯฮนฮฟฯ ฮฑฮฝฯฮฏฯฯฮฟฮนฯฮฑ.
ฮ.1.ฮฮนฮฑฮผฮฟฯฯฯฯฯฮต ฯฮฑ ฮดฮนฮบฮฌ ฯฮฑฯ ฮตฯฯฯฮฎฮผฮฑฯฮฑ ฯฮฟฯ ฮท ฮฑฯฮฌฮฝฯฮทฯฮฎ ฯฮฟฯ ฯ ฮตฯฮนฮฒฮฌฮปฮปฮตฮน ฯฮท ฮดฮนฮฑฮผฯฯฯฯฯฮท ฯฯฮฝ ฮดฯฮฟ ฮณฯฮฑฯฮนฮบฯฮฝ ฯฮฑฯฮฑฯฯฮฌฯฮตฯฮฝ (ฮณฮนฮฑ ฯฮฑฯฮฌฮดฮตฮนฮณฮผฮฑ, ฯฮฑ ฯฮฑฮนฮดฮนฮฌ ฮฝฮฑ ฯฯ ฮฝฮฑฮฝฯฮนฮฟฯฮฝฯฮฑฮน ฯฯฮตฮนฯ ฯฮฟฯฮญฯ, ฮฝฮฑ ฮบฮนฮฝฮฟฯฮฝฯฮฑฮน ฮตฯ ฮธฯฮณฯฮฑฮผฮผฮฑ ฮบฮฑฮน ฮฟฮผฮฑฮปฮฌ ฮบ.ฮป.ฯ.).
ฮ.2. โฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆโฆ.
(Tฮฟ project ฮฑฮฝฮฑฯฯฮฎฮธฮทฮบฮต ฯฯฮทฮฝ ฮฮฟฮนฮฝฯฯฮทฯฮฑ ฯฮฟฯ Scratch ฯฮฟ ฮฮฟฮญฮผฮฒฯฮท ฯฮฟฯ 2013 https://scratch.mit.edu/projects/13973896/ )
ฮฃฮทฮผฮตฮฏฯฯฮท 1. ฮฮน ฮญฮพฮน ฯฯฮฟฯฮตฮนฮฝฯฮผฮตฮฝฮตฯ ฮบฮฑฯฮทฮณฮฟฯฮฏฮตฯ ฮดฯฮฑฯฯฮทฯฮนฮฟฯฮฎฯฯฮฝ ฯฯ ฮฝฮฟฮดฮตฯฮฟฮฝฯฮฑฮน ฮฑฯฯ ฯฮนฯ ฯฮตฮปฮฏฮดฮตฯ ฮฟฮธฯฮฝฮทฯ ฯฮฟฯ ยซฮญฯฯฯฮฑยป ฮบฮฑฮธฯฯ ฮดฮนฮฑฮผฯฯฯฯฮฝฮฑ ฯฮนฯ ฮดฯฮฑฯฯฮทฯฮนฯฯฮทฯฮตฯ ฮบฮฑฮน ฮตฮฏฮฝฮฑฮน ฮตฮฝฮดฮตฮนฮบฯฮนฮบฮญฯ. ฮคฮตฮปฮตฮนฯฮฝฮฟฮฝฯฮฑฯ ฮฑฯ ฯฮฎ ฯฮทฮฝ ฮตฯฮณฮฑฯฮฏฮฑ ฮดฮนฮฑฯฮฏฯฯฯฯฮฑ ฯฮฟฮฝ ฯฮปฮฟฯฯฮฟ ฯฯฮฝ ฮดฯ ฮฝฮฑฯฮฟฯฮฎฯฯฮฝ ฯฮฟฯ ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฯฯฮฟฯฯฮญฯฮฟฯ ฮฝ ฮดฯฮฟ ฯฯฯฮฟ ฮผฮนฮบฯฮฌ ฮตฮพฮตฮนฮดฮนฮบฮตฯ ฮผฮญฮฝฮฑ applets Scratchโฆ
ฮฃฮทฮผฮตฮฏฯฯฮท 2. ฮฯฮฟฮนฮฟฯ ฮตฮฝฮดฮนฮฑฯฮญฯฮตฯฮฑฮน ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฮดฮตฮน ฯฮฟฮฝ ฮบฯฮดฮนฮบฮฑ ฯฯฮฟฮณฯฮฑฮผฮผฮฑฯฮนฯฮผฮฟฯ ฮตฮฝฯฯ Scratch project ฮบฮฑฯฮตฮฒฮฌฮถฮฟฮฝฯฮฑฯ ฯฮฟ ฮฑฯฯฮตฮฏฮฟ ฮฑฯฯ ฯฮฟ Scratch Website ฮฑฯฮฟฯ ฯฯฯฯฮฑ ฮญฯฮตฮน ฮบฮฑฯฮตฮฒฮฌฯฮตฮน ฯฯฮฟฮฝ ฯ ฯฮฟฮปฮฟฮณฮนฯฯฮฎ ฯฮฟฯ ฯฮฟ ฮตฮปฮตฯฮธฮตฯฮฟ ฮปฮฟฮณฮนฯฮผฮนฮบฯ ฮฑฯฯ ฯฮฟย http://www.scratch.mit.edu/ย ย ย . ฮฃฯฮท ฯฯ ฮฝฮญฯฮตฮนฮฑ ฮผฯฮฟฯฮตฮฏ ฮฝฮฑ ฯฮฟ ฯฯฮญฮพฮตฮน ฯฮต ฮฟฮปฯฮบฮปฮทฯฮท ฯฮทฮฝ ฮฟฮธฯฮฝฮท ฮผฮต ฮบฮปฮนฮบ ฯฯฮฟ ฮบฮฟฯ ฮผฯฮฏ ฮ ฮตฯฮนฮฒฮฌฮปฮปฮฟฮฝ ฮ ฮฑฯฮฟฯ ฯฮฏฮฑฯฮทฯ ฯฮฟฯ ฮฒฯฮฏฯฮบฮตฯฮฑฮน ฯฯฮฟ ฯฮฌฮฝฯ ฮดฮตฮพฮฏ ฮผฮญฯฮฟฯ ฯฮทฯ ฮฟฮธฯฮฝฮทฯ ฮฎ ฮฝฮฑ ฯฮฟ ฮฑฮพฮนฮฟฯฮฟฮนฮฎฯฮตฮน ฮผฮต ฮฒฮนฮฝฯฮตฮฟฯฯฮฟฮฒฮฟฮปฮญฮฑ ฮฎ ฮดฮนฮฑฮดฯฮฑฯฯฮนฮบฯ ฯฮฏฮฝฮฑฮบฮฑ (ฮตฯฯฯฮฟฮฝ ฮตฮฝฮดฮตฮฏฮบฮฝฯ ฯฮฑฮน).
ฮฮฟฮนฮฝฮฟฯฮฟฮนฮฎฯฯฮต:
ฮฃฯฮตฯฮนฮบฮฌ
By eduportal • ฮฮนฮดฮฑฮบฯฮนฮบฮฎ • 0 • Tags: applet, ฮบฮนฮฝฮทฮผฮฑฯฮนฮบฮฎ, ฮฮฏฮบฮฟฯ ฮฮฑฯฯฮฝฯฮตฯ, ฯฮฟฮปฮปฮฑฯฮปฮญฯ ฮฑฮฝฮฑฯฮฑฯฮฑฯฯฮฌฯฮตฮนฯ, ฯฯ ฯฮนฮบฮญฯ ฮตฯฮนฯฯฮฎฮผฮตฯ